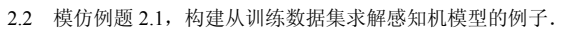统计学习方法L2
感知机(perceptron)是二类分类的线性分类模型,其输入为实例的特征向量,输出为实例的类别,取+1和-1二值
- 感知机对应于输入空间(特征空间)中将实例划分为正负两类的分离超平面,属于判别模型
- 感知机旨在求出训练数据进行线性划分的分离超平面
- 为此,导入基于误分类的损失函数,利用梯度下降法对损失函数进行极小化,求得感知机模型
- 感知机学习算法具有简单而易于实现的优点,分为原始形式和对偶形式
- 感知机预测是用学习得到的感知机模型对新的输入实例进行分类
本章内容
- 介绍感知机模型
- 叙述感知机的学习策略,特别是损失函数
- 介绍感知机学习算法,包括原始形式和对偶形式,并证明算法的收敛性
2.1 感知机模型
定义:假设输入空间(特征空间)是\(\chi \subseteq R^n\),输出空间是\(\gamma = \{+1, -1\}\)
- 输入\(x \in \chi\)表示实例的特征向量,对应于输入空间(特征空间)
- 输出\(y \in \gamma\)表示实例的类别
- 由输入空间到输出空间的如下函数称为感知机
\[ f(x) = sign(w \cdot x + b) \]
其中,\(w\)和\(b\)为感知机模型参数,前者\(w \in R^n\)为权值(weight)或权值向量(weight vector),后者\(b \in R\)为偏置(bias),\(w \cdot x\)表示\(w\)和\(x\)的内积
- sign是符号函数,即
\[ \begin{align*} sign(x)= \left \{ \begin{array}{ll} +1, & x \ge 0 \\ -1, & x \ < 0 \\ \end{array} \right. \end{align*} \]
- 感知机是一种线性分类模型,属于判别模型
- 假设空间是定义在特征空间中的所有线性分类模型(linear classification model)或线性分类器(linear classifier),即函数集合\(\{f \vert f(x)=w\cdot x + b \}\)
几何解释
- 对于线性方程\(w\cdot x+b = 0\)
- 对应于特征空间\(R^n\)中的一个超平面\(S\),其中\(w\)是超平面的法向量,\(b\)是超平面的截距
- 这个超平面将特征空间划分为两个部分
- 位于两部分的点(特征向量)分别被分为正、负两类
- 因此,超平面\(S\)被称为分离超平面(separating hyperplane)
感知机学习
由训练数据集(实例的特征向量及类别) \[ T= \{(x_1,y_1), (x_2,y_2),\dots,(x_N, y_N)\} \] 其中,\(x_i \in \chi = R^n, y_i\in \gamma= \{+1,-1\}, i=1,2,\dots,N\),即求得模型参数\(w, b\)。
感知机预测
通过学习得到的感知机模型,对于新的输入实例给出其对应的输出类别
2.2 感知机学习策略
数据集的线性可分性
- 给定训练数据集(实例的特征向量及类别)
\[ T= \{(x_1,y_1), (x_2,y_2),\dots,(x_N, y_N)\} \]
其中,\(x_i \in \chi = R^n, y_i\in \gamma= \{+1,-1\}, i=1,2,\dots,N\)
- 如果存在某个超平面S:\(w \cdot x + b = 0\)能够将数据集的正实例点和负实例点完全正确地划分到超平面的两侧
- 则称数据集\(T\)为线性可分数据集(linearly separable data set),否则称数据集\(T\)线性不可分
感知机学习策略
- 我们需要确定一个学习策略,即定义(经验)损失函数并将损失函数极小化
损失函数的一个自然选择是误分类点的总数
- 但是,这样的损失函数不是参数\(w,b\)的连续可导函数,不易优化
损失函数的另一个选择是误分类点到超平面\(S\)的总距离,这是感知机所采用的
- 输入空间中任一点\(x_0\)到超平面\(S\)的距离是
\[ \frac{1}{||w||}|w \cdot x_0 + b | \]
\(||w||\)是\(w\)的\(L_2\)范数
对于误分类的数据\((x_i, y_i)\)来说 ,\(-y_i(w \cdot x_i + b) > 0\)成立
- 误分类点\(x_i\)到超平面\(S\)的距离是
\[ -\frac{1}{||w||}y_i(w \cdot x_i + b) \]
所有误分类点(记为M)到超平面\(S\)的总距离为
\[ -\frac{1}{||w||}\sum_{x_i \in M}y_i(w \cdot x_i + b) \]
不考虑\(\frac{1}{||w||}\),就可以得到感知机学习的损失函数 \[ L(w,b) = - \sum_{x_i \in M}y_i(w \cdot x_i + b) \]
显然,损失函数\(L(w,b)\)是非负的
- 如果没有误分类点,损失函数值是0
- 误分类点越少,误分类点离超平面越近,损失函数值就越小
一个特定的样本点的损失函数:
- 在误分类时是参数\(w,b\)的线性函数
- 在正确分类时是0
因此,给定训练数据集\(T\),损失函数\(L(w,b)\)是\(w,b\)的连续可导函数
2.3 感知机学习算法
感知机学习问题最优化的方法是随机梯度下降法
感知机学习算法的原始形式
损失函数最小化问题的解 \[ \min_{w,b}L(w,b) = - \sum_{x_i \in M}y_i(w \cdot x_i + b) \]
感知机学习算法是误分类驱动的,具体采用随机梯度下降法(stochastic gradient descent)
- 首先,任意选取一个超平面\(w_0,b_o\)
- 然后用梯度下降法不断地极小化目标函数,即上面的式子
- 极小化过程中不是一次使M中所有误分类点的梯度下降,而是一次随机选取一个误分类点使其梯度下降
- 损失函数\(L(w,b)\)的梯度由下面式子给出(假设误分类点集合\(M\)是固定的)
\[ \bigtriangledown_wL(w,b) = -\sum_{x_i \in M}y_ix_i \\ \bigtriangledown_bL(w,b) = -\sum_{x_i \in M}y_i \]
- 随机选取一个误分类点\((x_i, y_i)\),对\(w,b\)进行更新
\[ w \leftarrow w + \eta y_ix_i \\ b \leftarrow b + \eta y_i \]
其中,\(\eta\)是步长,在统计学习中又称为学习率(learning rate)
- 这样通过迭代可以期待损失函数\(L(w,b)\)不断减小,直到为0
算法如下:

- 该算法有如下解释:
- 当一个实例点被误分类,即位于分离超平面的错误一侧时,则调整\(w,b\)的值,使分离超平面向该误分类点的一侧移动,以减少该误分类点与超平面间的距离,直到超平面越过该误分类点使其被正确分类
算法的收敛性
证明,对于线性可分数据集感知机学习算法原始形式收敛,即经过有限次迭代可以得到一个将训练数据集完全正确划分的分离超平面及感知机模型




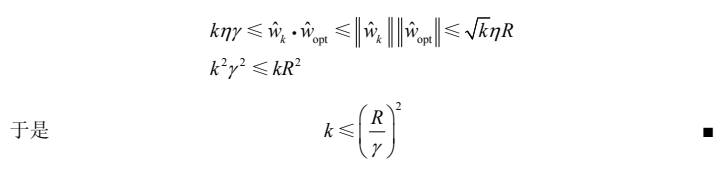
- 定理表明,误分类的次数\(k\)是有上限的,经过有限次搜索可以找到训练数据完全正确分开的分离超平面。
- 即,当训练数据集线性可分时,感知机学习算法原始形式迭代是收敛的
- 当训练集线性不可分时,感知机学习算法不收敛,迭代结果会发生震荡
感知机学习算法的对偶形式
对偶形式的基本想法:将\(w\)和\(b\)表示为实例\(x_i\)和标记\(y_i\)的线性组合的形式,通过求解其系数而求得\(w\)和\(b\)
对误分类点\((x_i, y_i)\)通过 \[ w \leftarrow w + \eta y_ix_i \\ b \leftarrow b + \eta y_i \] 逐步修改\(w, b\),设修改\(n\)次,则\(w, b\)关于\((x_i, y_i)\)的增量分别是\(\alpha_iy_ix_i\)和\(\alpha_iy_i\),这里的\(\alpha_i = n_i\eta\)
- 这样可以看出,学习到的\(w, b\)可以分别表示为
\[ w = \sum_{i=1}^N\alpha_iy_ix_i \\ b = \sum_{i=1}^N\alpha_iy_i \]
注意,这里的点对是误分类点,关于\((x_i, y_i)\)这个点对$w, b $进行修改
- \(\alpha_i > 0 , i = 1, 2, \dots, N\),当\(\eta\)等于1时,表示第\(i\)个实例点由于误分而进行更新的次数
- 实例点更新次数越多,意味着它距离分离超平面越近,也就越难正确分类,换句话说,这样的实例对学习结果影响最大
算法如下:


\(w\)用\(\sum_{j=1}^N \alpha_jy_jx_j\)表示,更新\(\alpha\)和\(b\)
对偶形式中训练实例仅以内积的形式出现
- 为了方便,可以预先将训练集中实例间的内积计算出来并以矩阵的形式存储,这个矩阵就是所谓的\(Gram\)矩阵(Gram matrix) \[ G = [x_i \cdot x_j]_{N \times N} \]
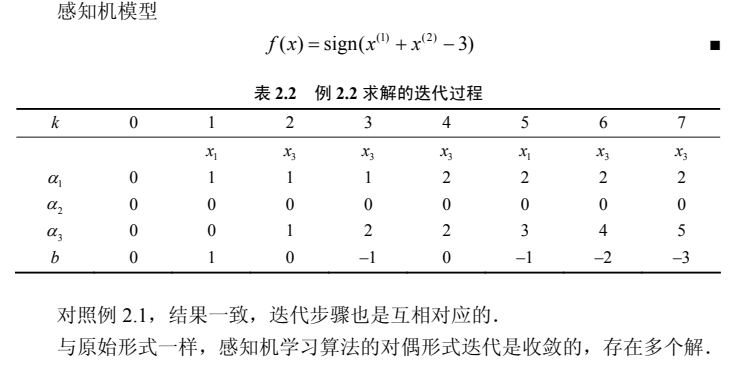
例子

本章概要

习题

| \(x\) | \(y\) | \(x \oplus y\) |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
XOR表示的区域是对角是相同的输出,但是一根线,也就是一个超平面无法做出这样的划分