不变性

  • 卷积神经网络正是将空间不变性（spatial invariance）的这一概念系统化，从而基于这个模型使用较少的参数来学习有用的表示。

适合于计算机视觉的神经网络结构：

  1. 平移不变性（translation invariance）：不管检测对象出现在图像中的哪个位置，神经网络的前面几层应该对相同的图像区域具有相似的反应，即为“平移不变性”。
  2. 局部性（locality）：神经网络的前面几层应该只探索输入图像中的局部区域，而不过度在意图像中相隔较远区域的关系，这就是“局部性”原则。最终，在后续神经网络，整个图像级别上可以集成这些局部特征用于预测。

限制多层感知机

  • 多层感知机的输入：二维图像\(X\)
    • 隐藏表示\(H\)是一个矩阵，代码中表示为二维张量，其中X和H具有相同的形状
  • 可以认为，无论是输入还是隐藏表示都拥有空间结构

平移不变性

  • 意味着检测对象在输入\(X\)中的平移，应该仅仅导致隐藏表示\(H\)中的平移
  • 也就是说，\(V\)和\(U\)实际上不依赖于\((i, j)\)的值，即\([V]_{i,j,a,b}=[V]_{a,b}\)
  • 并且U是一个常数，比如u，所以可以将H定义简化为

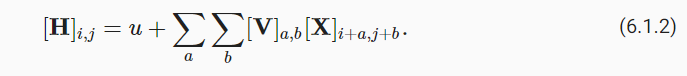
局部性

  • (6.1.3)是一个 卷积层 （convolutional layer），而卷积神经网络是包含卷积层的一类特殊的神经网络。
  • \(V\)被称为卷积核 （convolution kernel） 或者 滤波器 （filter），它仅仅是可学习的一个层的权重。

卷积神经网络和多层感知机的训练差异：

  • 以前，多层感知机可能需要数十亿个参数来表示网络中的一层，而现在卷积神经网络通常只需要几百个参数，而且不需要改变输入或隐藏表示的维数。
  • 参数大幅减少的代价是，我们的特征现在是平移不变的，并且当确定每个隐藏激活的值时，每一层只能包含局部的信息。
  • 以上所有的权重学习都将依赖于归纳偏置
  • 当这种偏置与现实相符时，我们就能得到样本有效的模型，并且这些模型能很好地泛化到未知数据中
  • 如果这偏置与现实不符时，比如当图像不满足平移不变时，我们的模型可能难以拟合我们的训练数据

卷积

通道

  • 图像不是二维张量，而是一个由高度、宽度和颜色组成的三维张量，比如包含1024×1024×3 个像素。
  • 前两个轴与像素的空间位置有关，而第三个轴可以看作是每个像素的多维表示。
  • 因此，我们将 XX索引为$ [X]_{i,j,k}$ 。由此卷积相应地调整为 \([V]_{a,b,c}\) ，而不是 \([V]_{a,b}\)
  • 由于输入图像是三维的，我们的隐藏表示 H 也最好采用三维张量。
  • 我们可以把隐藏表示想象为一系列具有二维张量的 通道 （channel）。 这些通道有时也被称为 特征映射 （feature maps），因为每个通道都向后续层提供一组空间化的学习特征。
  • 直观上你可以想象在靠近输入的底层，一些通道专门识别边，而其他通道专门识别纹理。