线性模型

  • 衡量预估质量

  • 训练数据

  • 参数学习

  • 显示解（只有线性回归有）

  • 总结

  • 基础优化方法

​ - 梯度下降

​ -

​ - 梯度是下降最快的地方

​ - 学习率的选择

​ - 不能太小，也不能太大

​ -

​ - 小批量随机梯度下降

​ -

​ - 选择批量大小

​ -

  • 总结

从零开始实现线性回归

自己构建

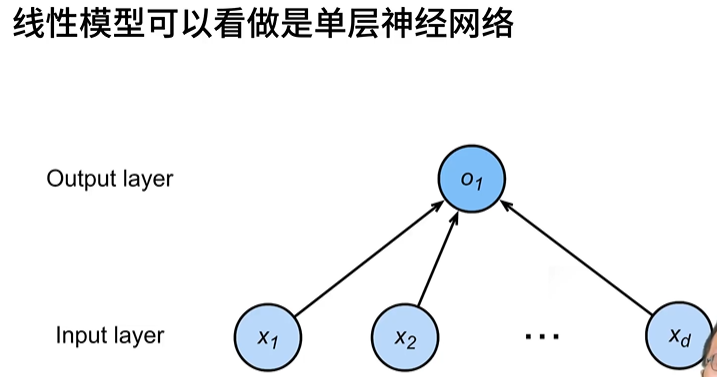
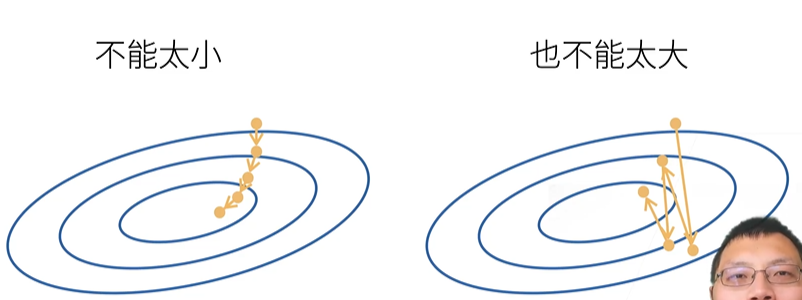
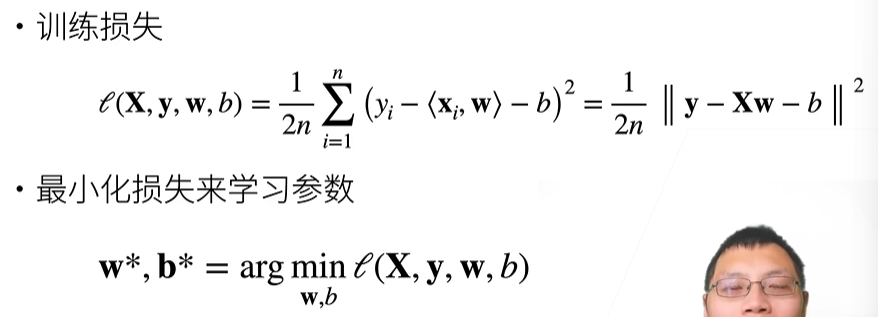1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
import os

import random

import torch

from d2l import torch as d2l

import matplotlib 

os.environ['KMP_DUPLICATE_LIB_OK'] = 'TRUE'

# y = Xw + b + e

# 根据带有噪声的线性模型构造一个的人造数据集

def synthetic_data(w, b, num_examples):

    # 均值为0，方差为1，大小

    X = torch.normal(0, 1, (num_examples, len(w)))

    y = torch.matmul(X, w) + b 

    y += torch.normal(0, 0.01, y.shape) # 加入噪音

    return X, y.reshape((-1, 1)) # 做成一个列向量返回



# 接受批量大小、特征矩阵和标签向量作为输入

# 输出大小为batch_size的小批量

def data_iter(batch_size, features, labels):

    num_examples = len(features)

    indices = list(range(num_examples))

    # 样本是随机读取的，没有特定的顺序

    random.shuffle(indices)

    for i in range(0, num_examples, batch_size):

        batch_indices = torch.tensor(

            indices[i:min(i + batch_size, num_examples)])

        yield features[batch_indices], labels[batch_indices]



true_w = torch.tensor([2, -3.4])

true_b = 4.2

features, labels = synthetic_data(true_w, true_b, 1000)





# 查看特征和标签的相关性

# d2l.set_figsize()

# d2l.plt.scatter(features[:, 1].detach().numpy(),

#                 labels.detach().numpy(), 1)

# d2l.plt.show()



batch_size = 10



# 定义初始化模型参数

w = torch.normal(0, 0.01, size=(2, 1), requires_grad=True)

b = torch.zeros(1, requires_grad=True)



# 定义模型

def linreg(X, w, b):

    '''线性回归模型'''

    return torch.matmul(X, w) + b



# 定义损失函数

def squared_loss(y_hat, y):

    '''均方损失'''

    return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2



# 定义优化算法

def sgd(params, lr, batch_size):

    '''小批量随机梯度下降'''

    with torch.no_grad():

        for param in params:

            param -= lr * param.grad / batch_size

            param.grad.zero_()



# 训练过程

lr = 0.03 # 学习率

num_epochs = 3

net = linreg

loss = squared_loss



for epoch in range(num_epochs):

    for X, y in data_iter(batch_size, features, labels):

        l = loss(net(X, w, b), y) # x和y的小批量损失

        # 因为l形状是（batch_size, 1），而不是一个标量。

        # l中的所有元素被加到一起

        # 并以此计算关于[w, b]的梯度



        l.sum().backward()

        sgd([w, b], lr, batch_size)

    with torch.no_grad():

        train_l = loss(net(features, w, b), labels)

        print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')

使用模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
import numpy as np

import torch 

from torch.utils import data

from d2l import torch as d2l



true_w = torch.tensor([2, -3.4])

true_b = 4.2

features, labels = d2l.synthetic_data(true_w, true_b, 1000)



def load_array(data_arrays, batch_size, is_train=True):

    '''构造一个PyTorch的数据迭代器'''

    dataset = data.TensorDataset(*data_arrays)

    return data.DataLoader(dataset, batch_size, shuffle=is_train)



batch_size = 10

data_iter = load_array((features, labels), batch_size)



next(iter(data_iter))



# 使用框架的预定义好的层

# 'nn'是神经网络的缩写

from torch import nn

net = nn.Sequential(nn.Linear(2, 1)) # 输入二维，输出一维



# 初始化模型参数

net[0].weight.data.normal_(0, 0.01)

net[0].bias.data.fill_(0)



# 均方误差

loss = nn.MSELoss()



# SGD

trainer = torch.optim.SGD(net.parameters(), lr=0.03)



num_epochs = 3

for epoch in range(num_epochs):

    for X, y in data_iter:

        l = loss(net(X), y)

        trainer.zero_grad()

        l.backward()

        trainer.step()

    l = loss(net(features), labels)

    print(f'epoch {epoch + 1}, loss {l:f}')