扫描转换(Scan Conversion)

就是几何图元的扫描转换(线段,圆,多边形,椭圆等)

  • 在点阵中找到图元的最优近似点集
  • 从连续的图元到离散像素集合的映射
  • 本质上是一个采样问题

例子：线段(0,0)到(5,3)，最优点集：点到直线上的距离最小

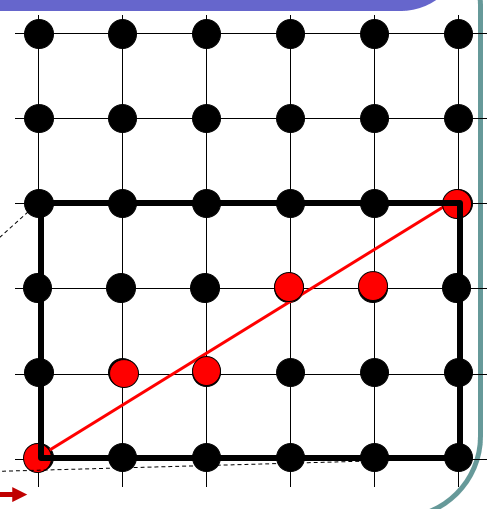
线段扫描转换(Scan conversion of line segments)

平凡算法

  • 缺点：多次乘法运算，取整运算

DDA算法--Digital differential analyzer

  • 缺点：仍然需要取整

Bresenham算法

  • 下一次可选点的约束

    • 当前像素一旦确定，下一个点是有限制的，只能从两个点中选一个
    • 算法只涉及+、-、移位
    • 用于绘图仪、显卡等硬件实现

  • 缩小可选点的范围

    • 从 \(x = x_0\)出发，每次增加1

    • 选中的第i个像素点为(\(\bar{x}_i, \bar{y}_i\))

    • 第\(i+1\)个像素点只能从2个点中选择

      • (\(\bar{x}_i + 1, \bar{y}_i\))，(\(\bar{x}_i + 1, \bar{y}_i + 1\))

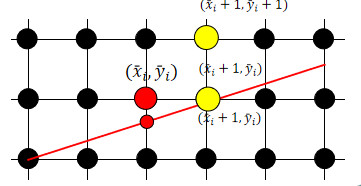
    • 选点判定准则(Criteria)

      • 选择离直线较近的那个像素点，即离\((x_{i+1}, y_{i+1})\)较近的点
        • \(x_{i+1} = x_i+1\)
        • \(y_{i+1} = mx_{i+1} +B = mx_i+m+B\)
      • 判别准则计算
      • 化简
      • \(p_i\)的迭代公式
      • \(p_0\)的计算

    • 例子

多边形扫描转换(Scan conversion of polygon)

  • 光栅图形的本质：点阵表示
    • 线框多边形物体：只需扫描转换线段
    • 填充多边形物体：要扫描转换多边形
  • 线框图：先扫描转换
  • 简单的多边形：无自相交
  • 图形学中多边形的两种表示方法
    • 顶点表示（对象表示）:多边形的有序顶点序列
      • 优点：直观,有几何意义、便于几何变换、存贮量小
      • 缺点：不能直接用于多边形着色
    • 点阵表示（图像表示）:多边形内部的像素集合

区域填充--Fill-area algorithms

多边形描线填充算法--Scan-line polygon-fill algorithm