李宏毅深度学习L2
机器学习的任务攻略
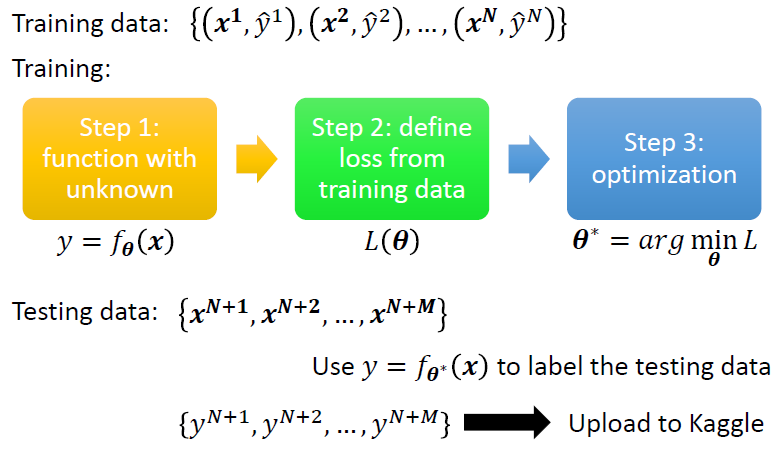
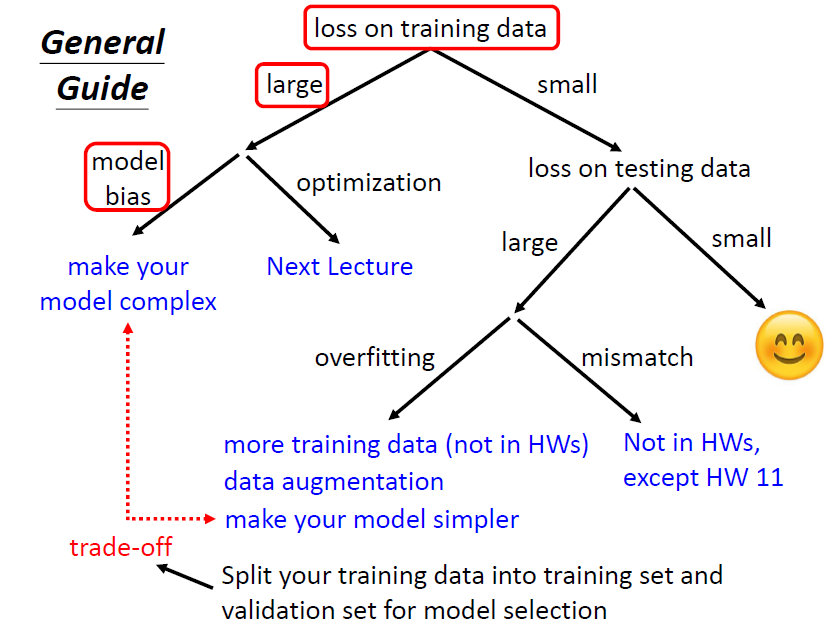
对于我们的模型,首先要保证训练损失在一个可接受的范围,才去考虑测试集损失的问题
根据训练损失过大做出的模型调整
当查看我们的训练损失过大的时候,需要调整我们的模型,有几个方向可以考虑
Model bias 模型偏差
问题
我们的模型可能过于简单,模型的参数取值范围内只能构建一个比较小的函数集,没办法满足我们的需求,也就是模型的弹性不够
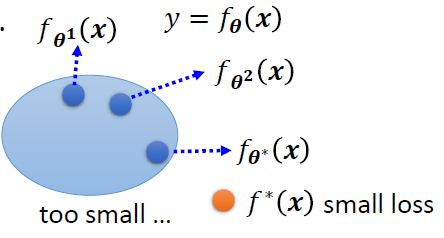
我们的最优解只是小范围函数集内的最优解
解决方案
重新设计模型,让它更加具有弹性,也就是范围更大

Optimization Issue 优化问题
问题
我们的模型使用优化方法是梯度下降,但是模型只是找到局部的最低点便停下来了
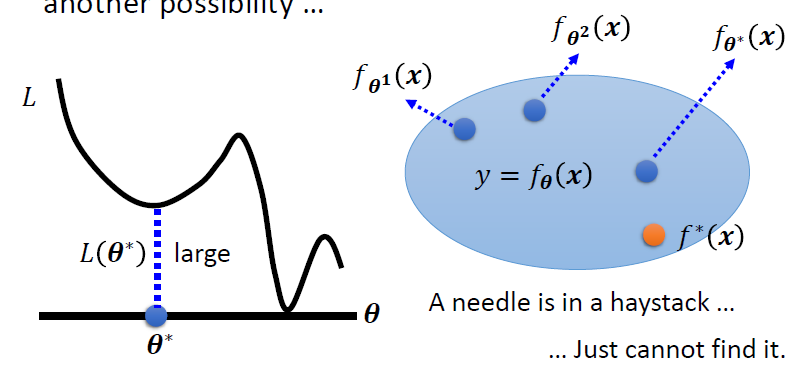
判断是Model Bias或者是Optimization Issue
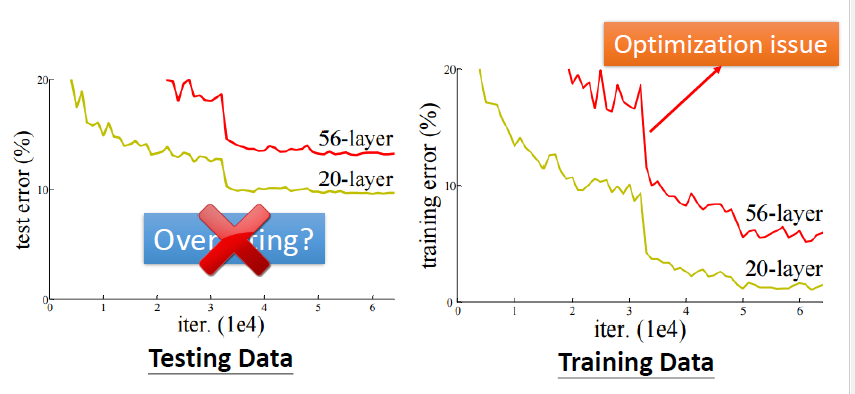
这并不是过拟合,因为在训练的数据集上,深层的损失也比浅层的损失大
在构建模型的过程中,我们可以先尝试浅层的模型,它们比较容易优化,再尝试比较深层的模型
如果深层的模型的损失比浅层的损失要大,说明是优化问题
根据测试集损失过大做出的模型调整
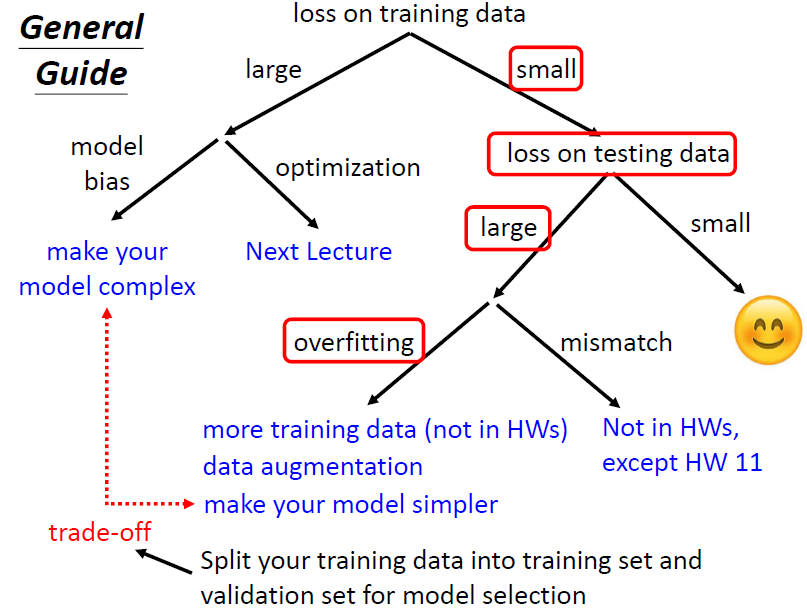
Overfitting 过拟合
在训练损失小,测试集损失很大的情况下,就是overfitting(过拟合)发生了
一个极端的例子

分析
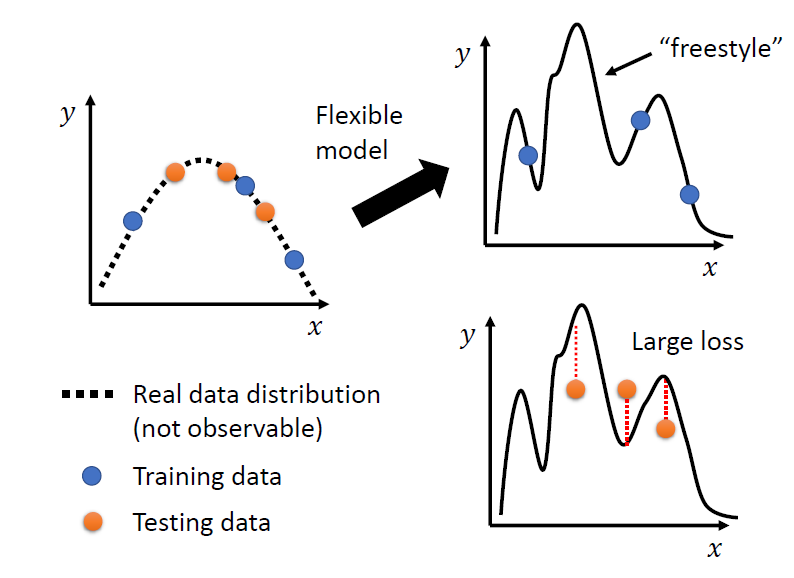
我们的数据是来自一个分布的,模型得到的函数会尝试根据所给的分布上的训练点集去拟合这个分布
解决
More training data 更多的训练数据集
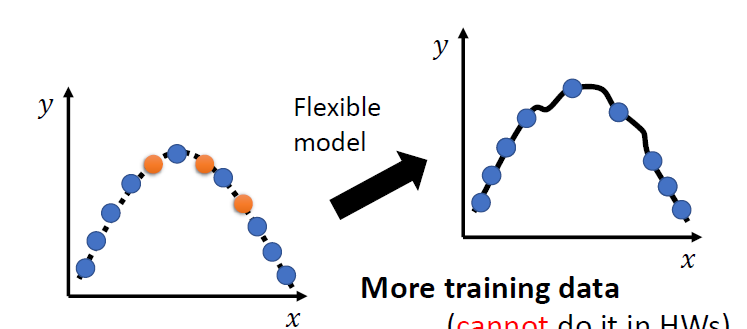
Data augmentation 数据增强

要合理,不要让模型学到奇怪的特征
constrained model 限制模型
我们知道数据的分布是二次函数时,可以限制模型为二次函数,得到比较好的结果
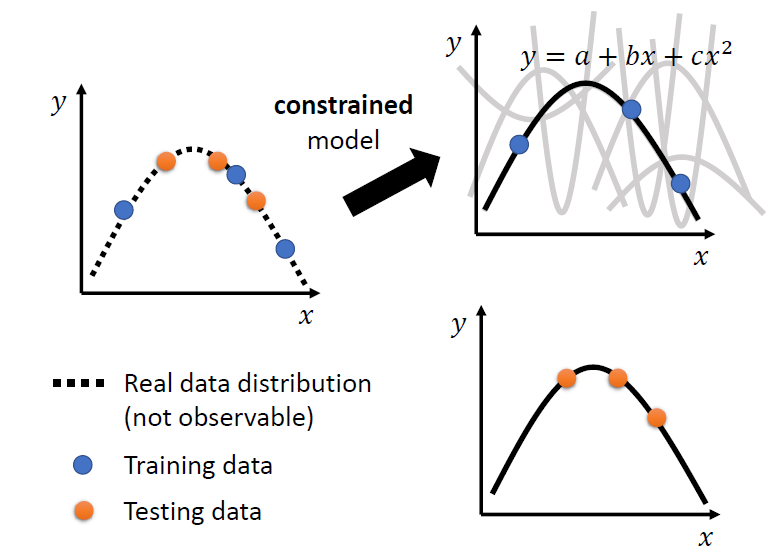
方法:
- 更少的参数,或者共享参数
- 更少的features
- Early stopping
- Regularization
- Dropout
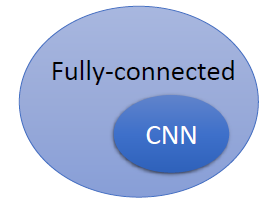
CNN限制比较大,针对图片和影像
但是也不能给模型太大的限制
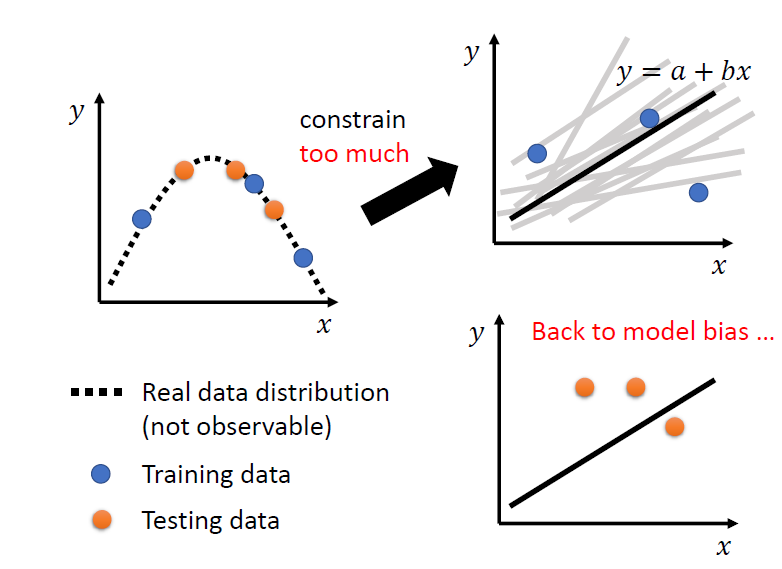
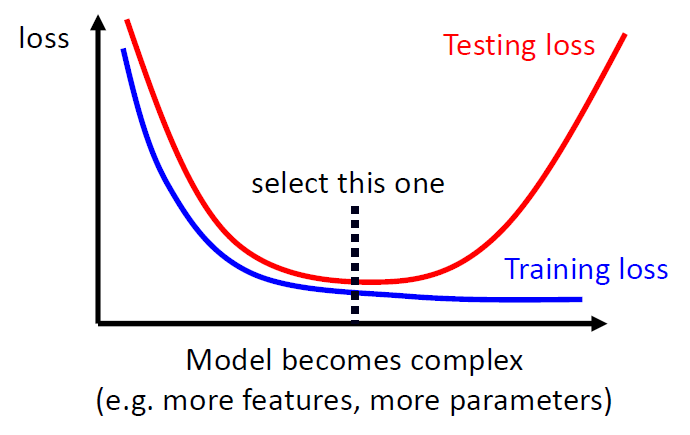
偏差-复杂度的权衡
Validation set
起因
Testing Set 有公开的和保密的,在训练模型时,大家会拿公开的Testing Set跑模型看结果怎么样,然后来调整模型,但是因为公开的Testing Set可以多次使用,可能会使你的模型对于公开的Testing Set更好地拟合,但是放到保密的Testing Set会得到比较糟糕的结果
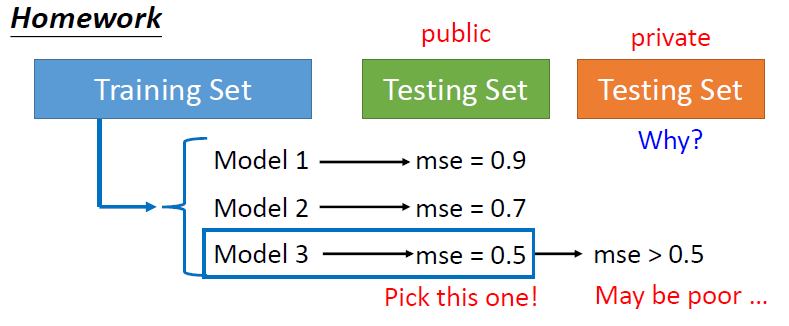
解决
可以将用于训练模型的数据Training Set分为两部分,即Training Set和Validation Set,在Training Set上跑了之后,用Validation Set作为验证来调整参数,其实它相当于前面公开的Testing Set,然后再用来跑公开的Testing Set,就是说不要去过度地根据公开的Testing Set去调整模型,这样,用来跑保密的Testing Set结果基本能够跟公开的保持一致
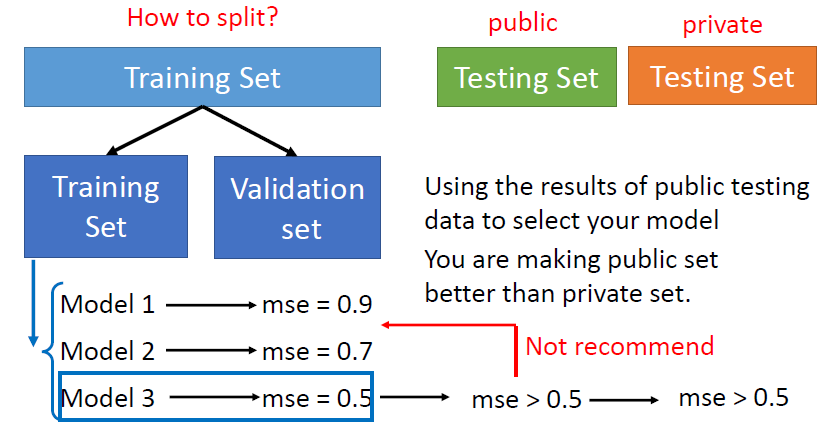
如何划分Training Set
方法:N fold Cross Validation
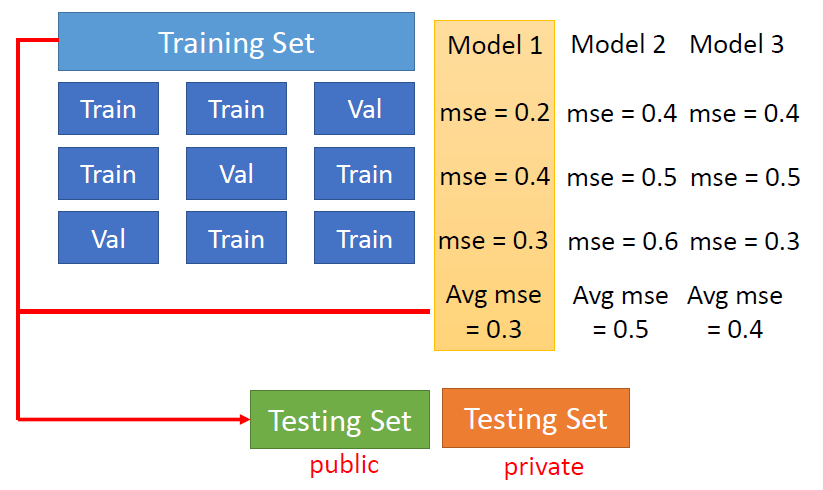
分成n段,轮流当Validation Set来进行训练
Mismatching 不一致
训练集和测试集的分布是不一致的

Critical Point
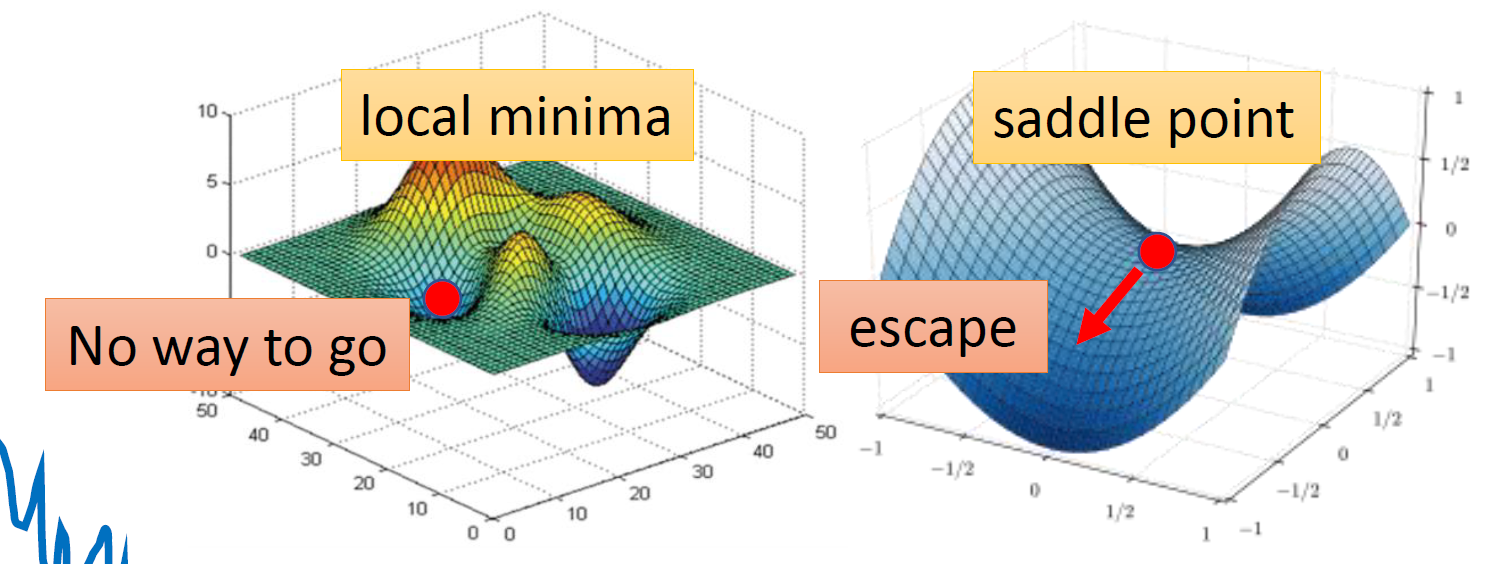
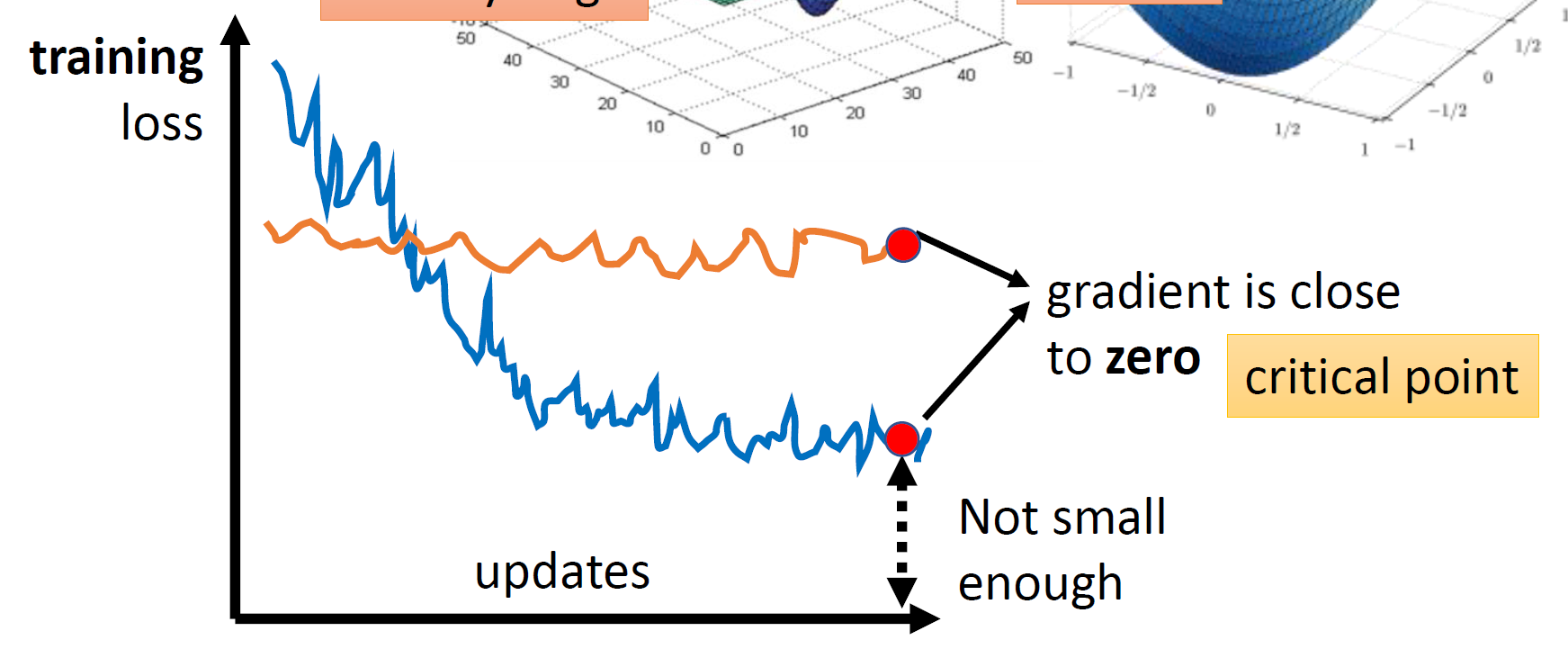
当梯度变得十分小的时候,Optimization会变得十分困难,这时候有两种情况:
- local minima 局部最小值
- saddle point 鞍点
它们统称为critical point
数学推导
泰勒近似
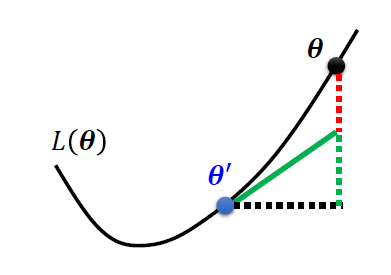
当\(\theta=\theta^{`}\)时,根据泰勒公式 \[ L(\theta) \approx L(\theta^{`}) + (\theta - \theta^{`})^{T}g + \frac{1}{2}(\theta-\theta^{`})^{T}H(\theta-\theta^{`}) \] 相当于函数泰勒公式中,f(x)在\(x_1\)处 \[ f(x) = f(x_1) + \frac{f^{`}(x_1)}{1!} (x-x_1) + \frac{f^{``}(x_1)}{2!}(x-x_1)^2 + o((x-x_1)^2) \] 其中,
g:Gradient(梯度) (下图中绿色部分)
是一个向量
\[ g = \nabla L(\theta^{`}) \\ g_i = \frac{\partial L(\theta^{`})}{\partial\theta_i} \]
\(g_i\)是损失函数对某一个参数的梯度
H:Hessian(下图中红色部分)
是一个矩阵
\[ H_{ij} = \frac{\partial^{2}}{\partial\theta_i\partial\theta_j}L(\theta^{`}) \]
而在Critical point上,g的部分等于0 \[
L(\theta) \approx L(\theta^{`}) + \frac{1}{2}(\theta-\theta^`)^TH(\theta
- \theta^`)
\] 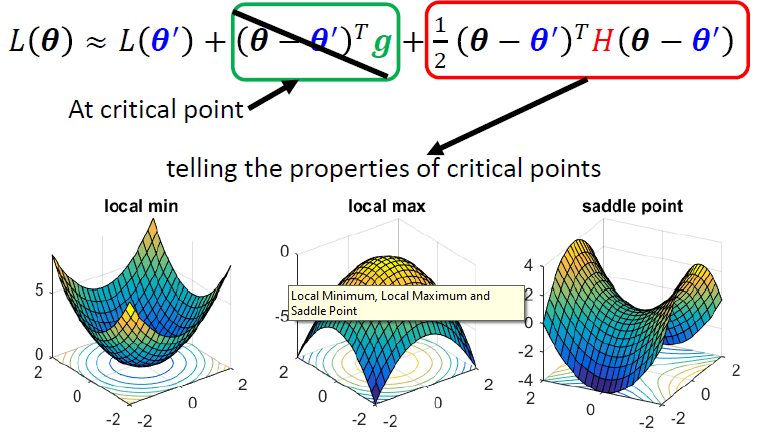
有三种情况:
- Local minima
- Local maxima
- Saddle point
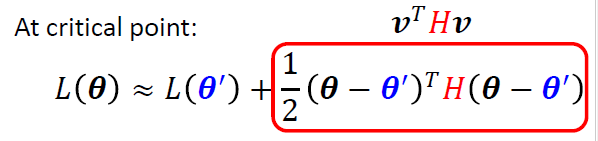
Local minima
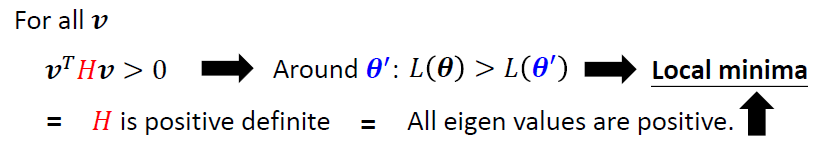
所有的特征值是正的
Local maxima
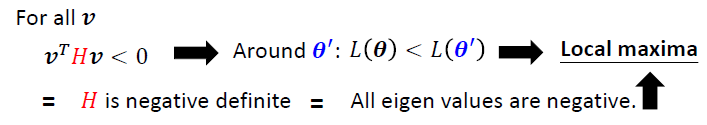
所有的特征值是负的
Saddle point
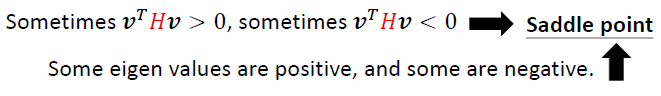
特征值有正有负
一个例子
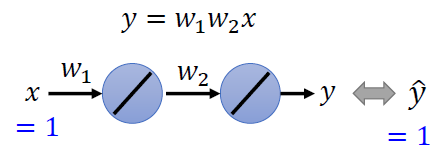
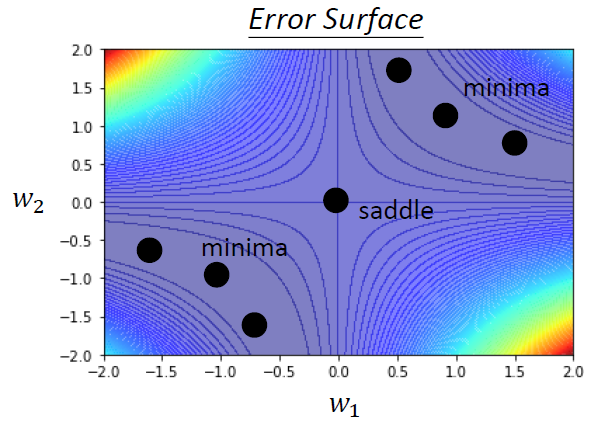
- 最优点(L最小)在(1, 1)和(-1, -1)这两个位置上
损失函数
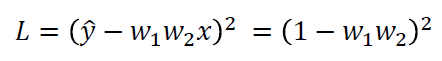
在(0, 0)处,

宝可梦、数码宝贝分类器
- 根据宝可梦和数码宝贝原画线条数目的多少可以来进行区分
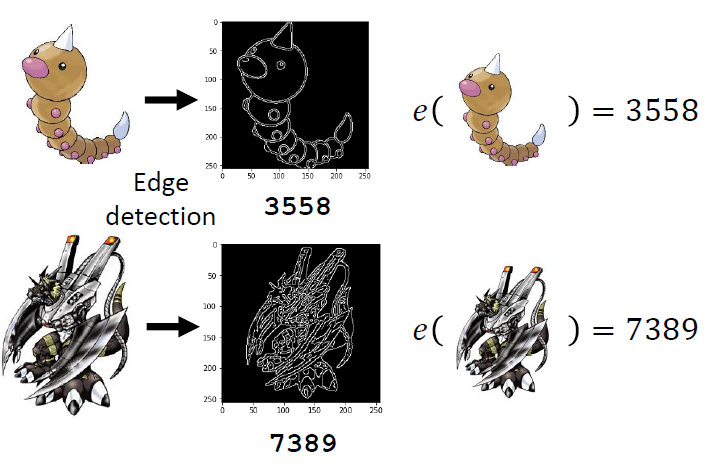
- 我们可以找到一个阈值h大于这个值为数码宝贝,小于这个值为宝可梦
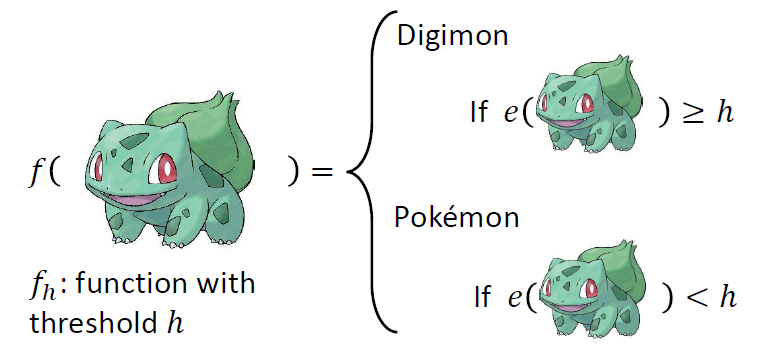
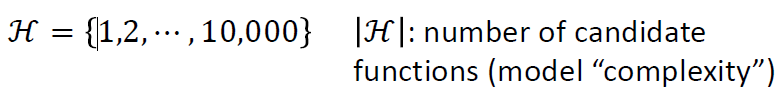
\(H\)是指候选函数的数目,即这个模型的复杂度,能够表达的函数集的大小
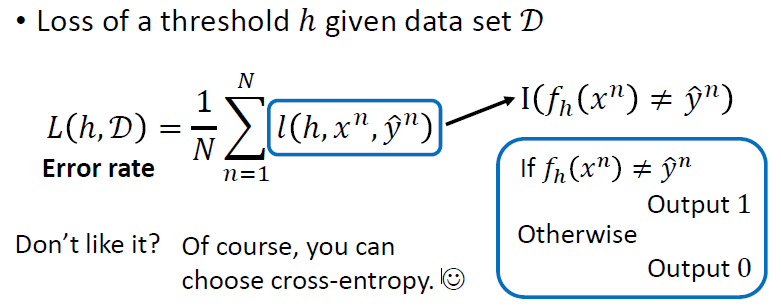
损失函数
使用的是错误率,也可以使用交叉熵
数据集和训练
- 数据集的形式
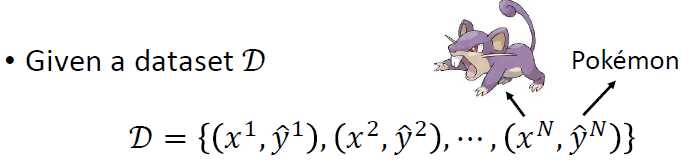
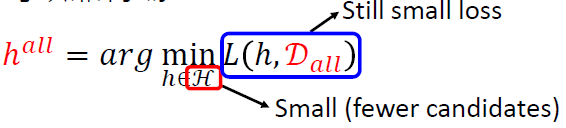
- 如果我们收集了所有的宝可梦和数码宝贝(记为\(D_{all}\)),我们可以找到最好的阈值(记为\(h^{all}\)),即
\[ h^{all} = arg \mathop{min}_{h}(h,D_{all}) \]
- 但现实是,我们一般只能从所有数据中获取到一部分数据,将其作为训练数据(记为\(D_{train}\))(独立且相同的分布)
\[ D_{train} = {(x^1, \hat{y}^1), (x^2, \hat{y}^2),\cdots (x^N, \hat{y}^N)} \\ \\ h^{train} = arg \mathop{min}_{h}(h, D_{train}) \]
- 我们希望的是训练得到的阈值\(h^{train}\)能够在整体的表现上能够接近\(h^{all}\),即
\[ L(h^{train}, D_{all}) \rightarrow L(h^{all}, D_{all}) \]
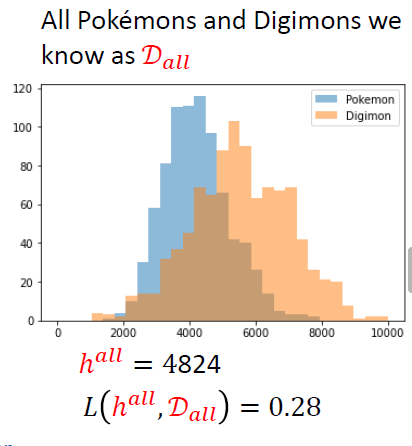
- 从所有的数据中我们得到\(h^{all}=4824\)
- 随机采样200个数据样本作为\(D_{train1}\),得到\(h_{train1}\)
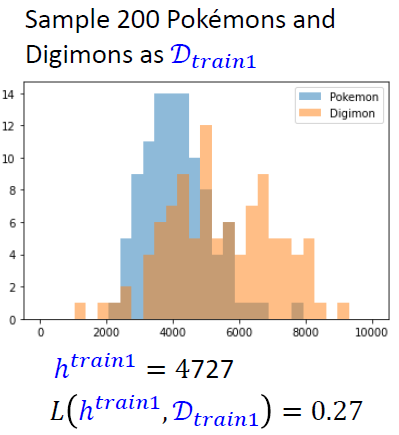
在总体上数据表现较好
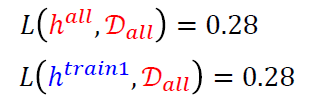
- 再随机采样200个数据样本作为\(D_{train2}\),得到\(h_{train2}\)
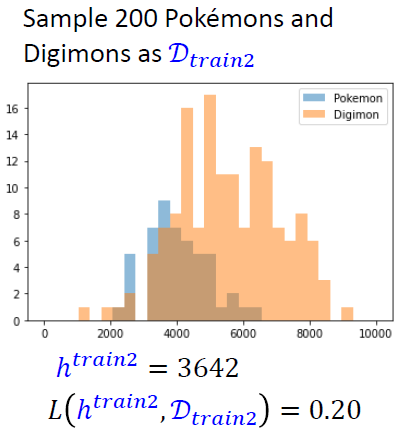
总体表现较差
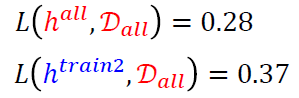
我们想要的是在训练集上训练得到的\(h^{train}\)能够在总体数据上表现能够接近理想中的\(h_{all}\) \[ L(h^{train}, D_{all}) \rightarrow L(h^{all}, D_{all}) \] 可以转化为 \[ L(h^{train}, D_{all}) - L(h^{all}, D_{all}) \le \delta \]
那么\(D_{train}\)要满足
\[ \forall h \in H, |L(h, D_{train}) - L(h, D_{all})| \le \delta/2 \]
上述公式的推导

我们想要的是好的\(D_{train}\),即
\[ \forall h \in H, |L(h, D_{train}) - L(h, D_{all})| \le \epsilon \\ \epsilon = \delta/2 \]
训练失败的概率
- 每一个点都是一个训练集
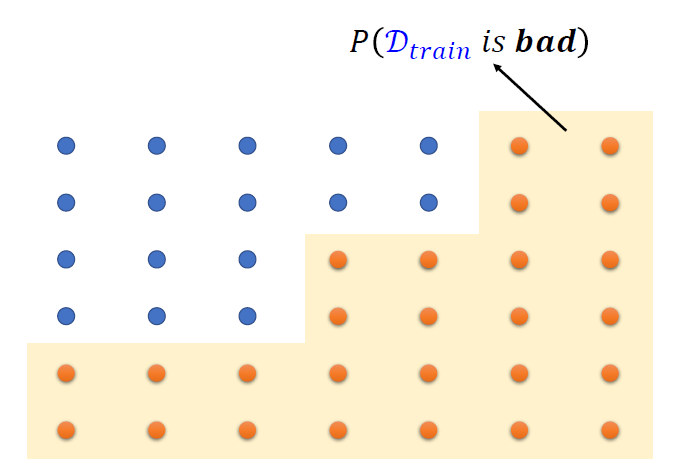
- 如果一个训练集\(D_{train}\)是坏的,至少有一个\(h\)会让
\[ |L(h, D_{train}) - L(h, D_{all})| \gt \epsilon \]
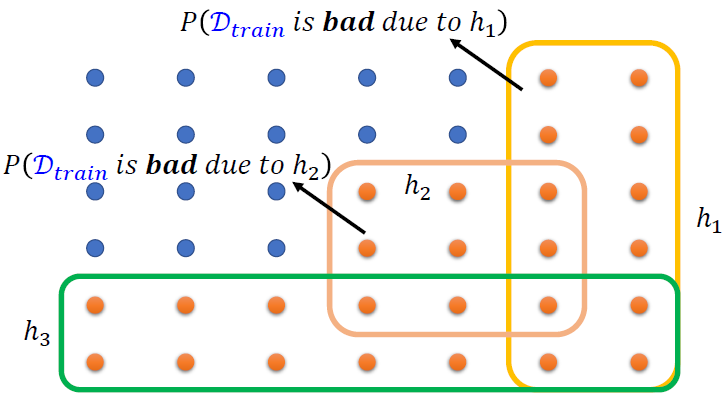 \[
P(D_{train}\ is \ bad) = \mathop\cup_{h\in H}P(D_{train} \ is \ bad \
due \ to \ h) \\
\le \mathop\sum_{h\in H}P(D_{train} \ is \ bad \ due \ to \ h)
\] 这里概率加起来是会大于1的,那说明会经常发生
\[
P(D_{train}\ is \ bad) = \mathop\cup_{h\in H}P(D_{train} \ is \ bad \
due \ to \ h) \\
\le \mathop\sum_{h\in H}P(D_{train} \ is \ bad \ due \ to \ h)
\] 这里概率加起来是会大于1的,那说明会经常发生
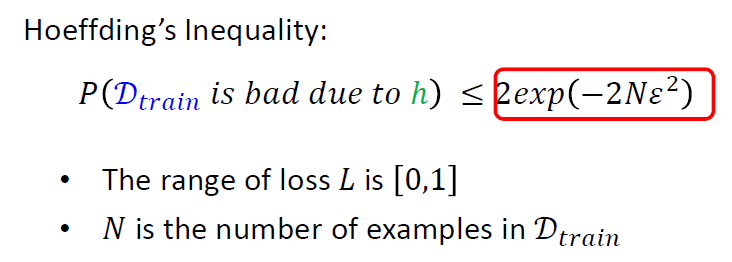
可以推导出

- 怎么使\(P(D_{train} \ is \
bad)\)变小
- 更大的N和更小的H
- 即更大的样本容量和更加简单或者说限制比较多的模型
- 更大的N
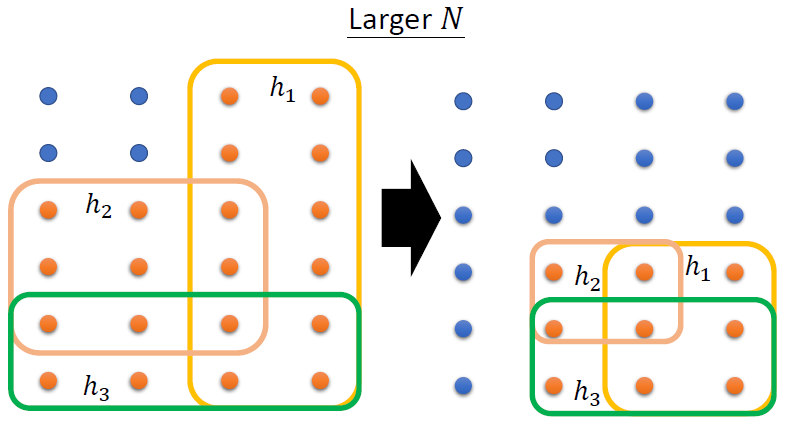
样本容量越大,越能够更好地接近总体的分布情况
- 更小的H
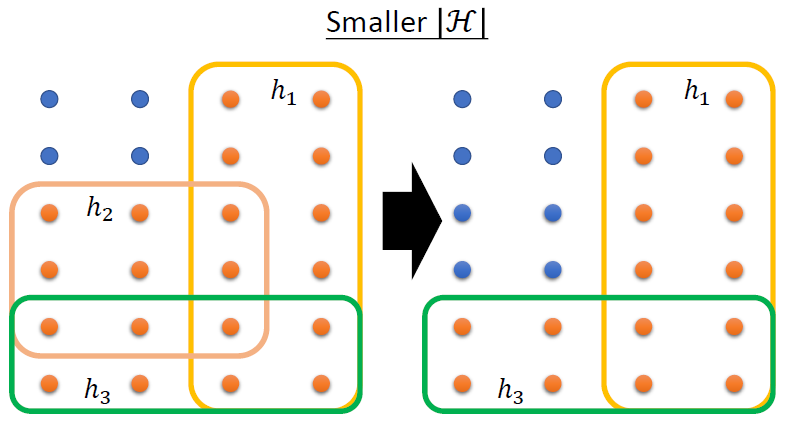
H变小了,那么参数h的数目就会变少,一些表现较差的参数也会被筛除
- 一个例子

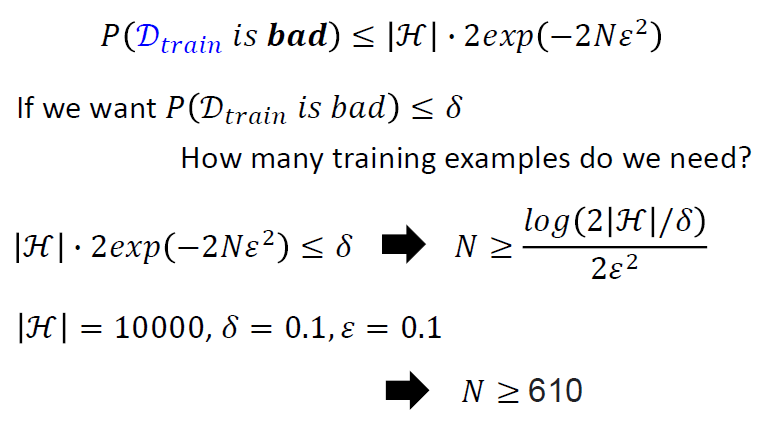
- 那如果模型的参数是连续的,该怎么选择
- 计算机内的一切都是离散的
- 如果使用更小的H就可以获取好的结果,那么为什么不直接使用很小的H

使用很小的H,我们的模型可能在数据上表现就是很差,去接近理想状态也没有意义
- 陷入了两难的境地
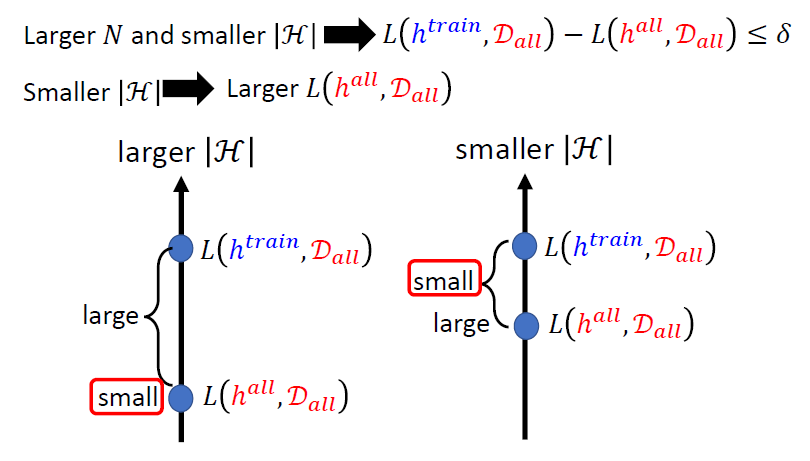
可以使用深度学习
训练的建议 -- Batch和Momentum
Batch 批量
批量优化
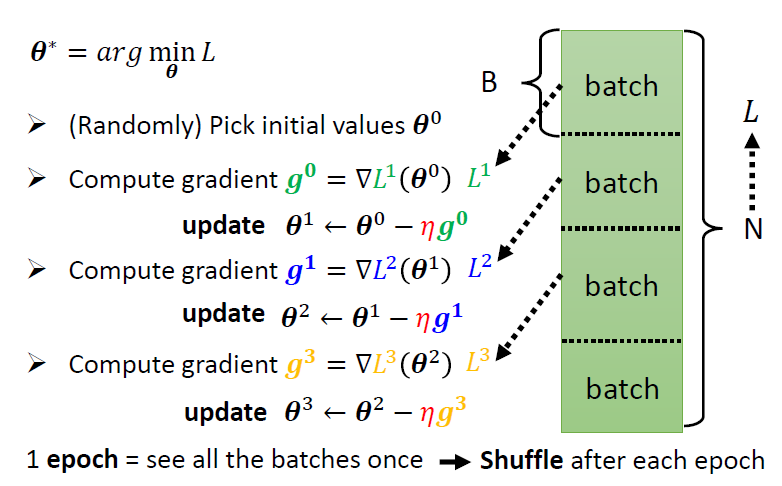
将一个数据集分成多个batch,可以多次更新参数
小的batch和大的batch
现在我们有20个样本(N=20)
- batch size = N = 20,即整个数据集
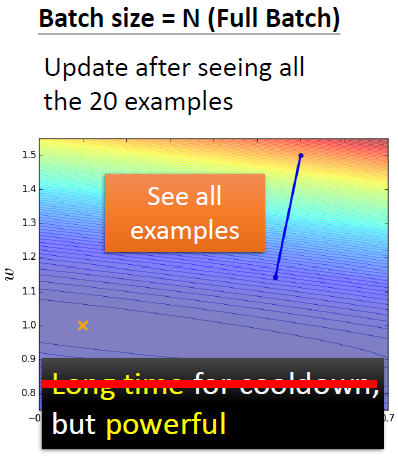
- batch size = 1

- 大的batch一般不需要更长的时间来计算梯度,除非batch实在太大了
- 小的batch需要更多的时间,在每一个epoch中计算梯度,即需要更多的时间来查看整个数据集
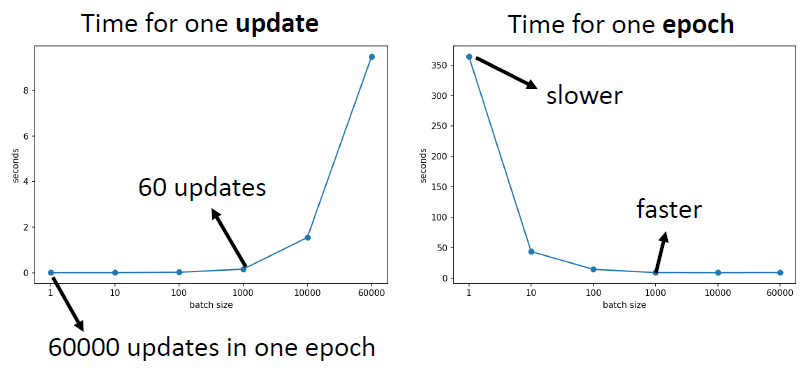
- 实例
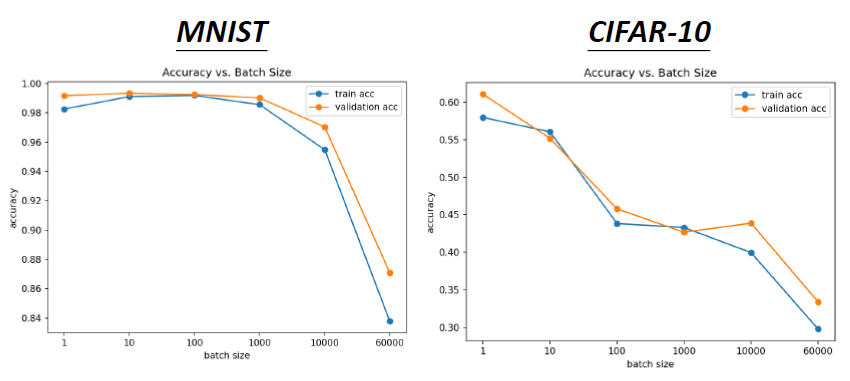
小的batch有着更好的表现,而大的batch可能会导致Optimizaiton Fails
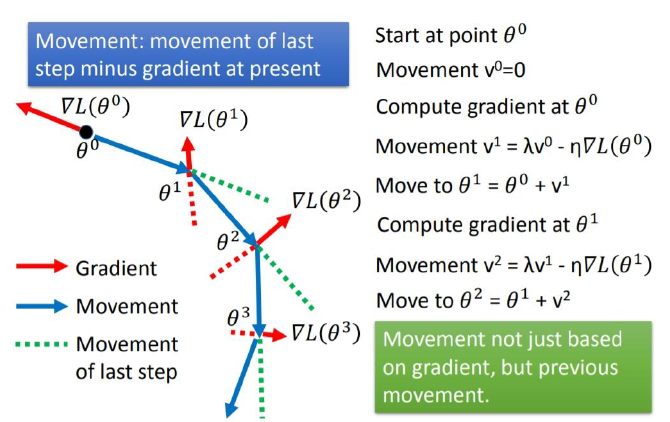
Momentum
- 让梯度下降保持一个动量,可以跨过平坦的Local minima
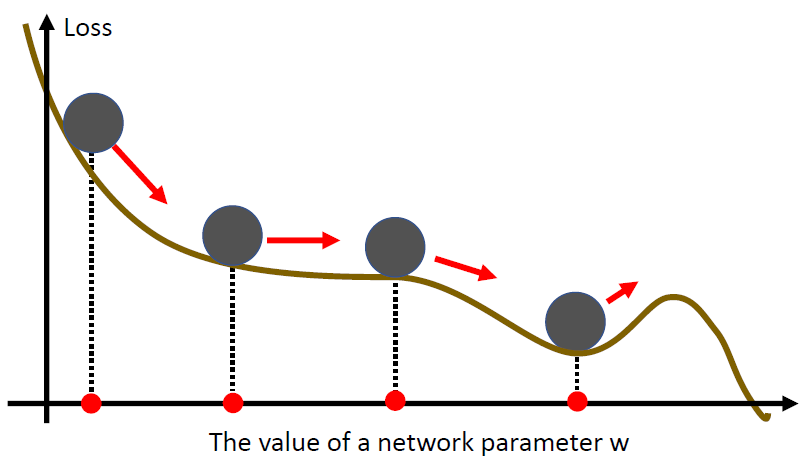
- 当前参数的变化不仅取决当前的梯度,还取决于之前的变化
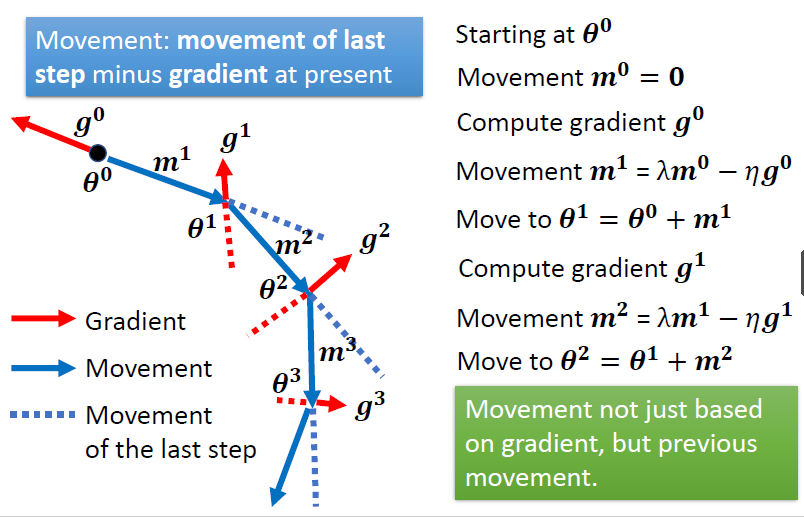
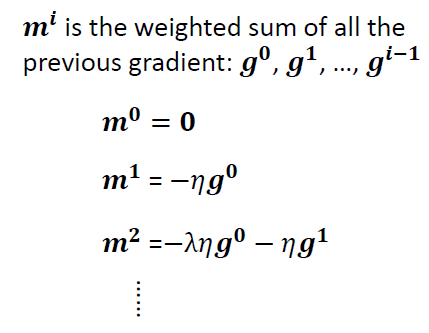
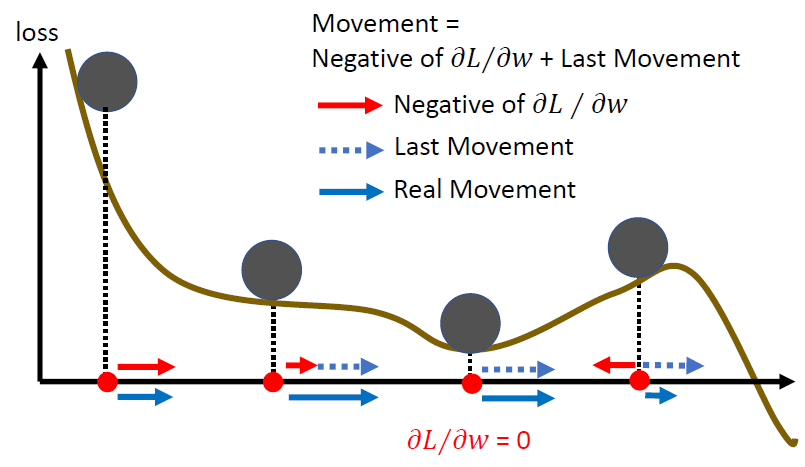
在损失函数到达一个比较平缓的梯度区间时,可以因为之前向右移动的趋势,而向右边移动
小结
小的batch size和Momentum可以帮助逃离critical points
Optimization的总结
一些符号标记
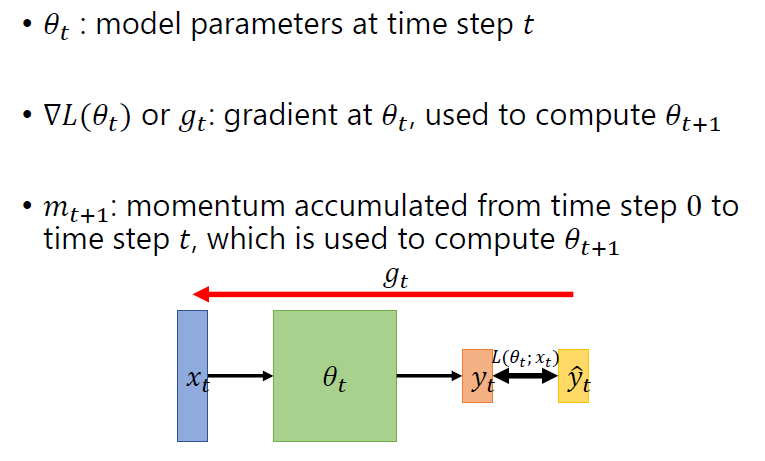
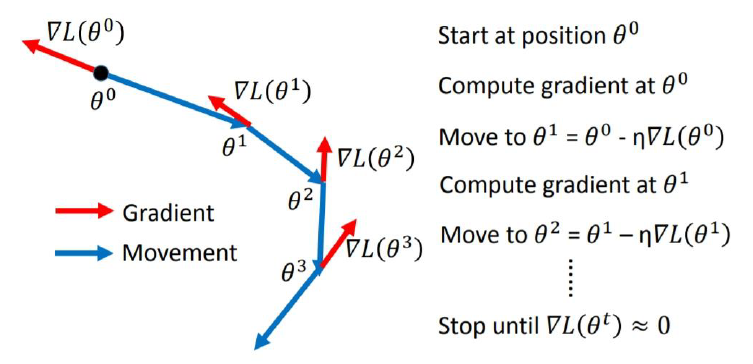
SGD
SGD with Momentum
\[ \theta_t = \theta_{t-1} - \eta m_t \\ m_t = \beta_1m_{t-1}+(1-\beta_1)g_{t-1} \]
Adagrad
\[ \theta_t = \theta_{t-1} - \frac{\eta}{\sqrt{\sum^{t-1}_{i=0}(g_i)^2}}g_{t-1} \]
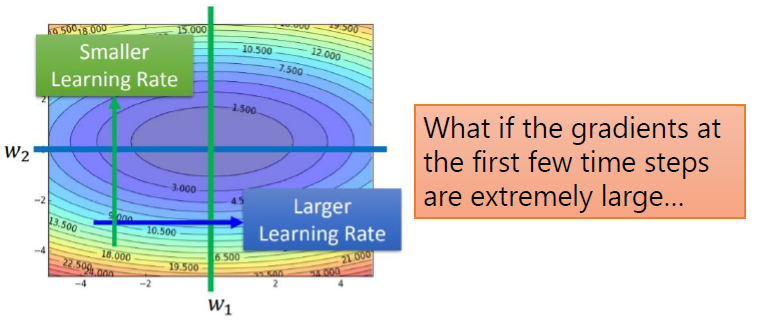
这种会累积之前所有的梯度,遇到一些需要你Learning Rate大的情况处理不了(如RMSProp中的图)
RMSProp
 \[
\theta_t = \theta_{t-1} - \frac{\eta}{\sqrt{v_t}}g_{t-1} \\
v_1 = g^2_0 \\
v_t = \alpha v_{t-1} + (1-\alpha)(g_{t-1})^2
\]
\[
\theta_t = \theta_{t-1} - \frac{\eta}{\sqrt{v_t}}g_{t-1} \\
v_1 = g^2_0 \\
v_t = \alpha v_{t-1} + (1-\alpha)(g_{t-1})^2
\]
Adam
- 是SGDM和RMSProp的结合
\[ \theta_t = \theta_{t-1} - \frac{\eta}{\sqrt{\hat{v_t}}+\epsilon}\hat{m_t} \]
\[ \hat{m_t} = \frac{m_t}{1-\beta_1^t} \\ \hat{v_t} = \frac{v_t}{1-\beta_2^t} \]
\[ \beta_1 = 0.9 \\ \beta_2 = 0.999 \\ \epsilon = 10^{-8} \]
Adam和SGDM的对比
- Adam
- 训练快速
- 较大的差别(训练集和测试集)
- 不稳定
- SGDM
- 稳定
- 很小的差别
- 更好的收敛
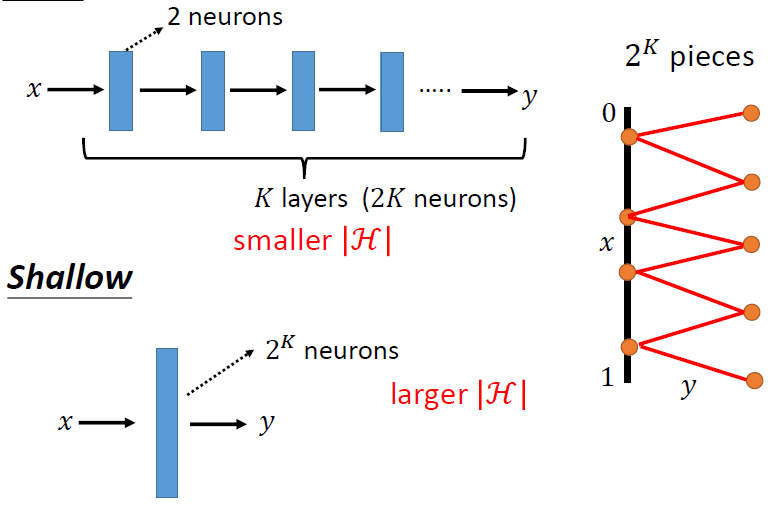
深度学习
我们想要的是
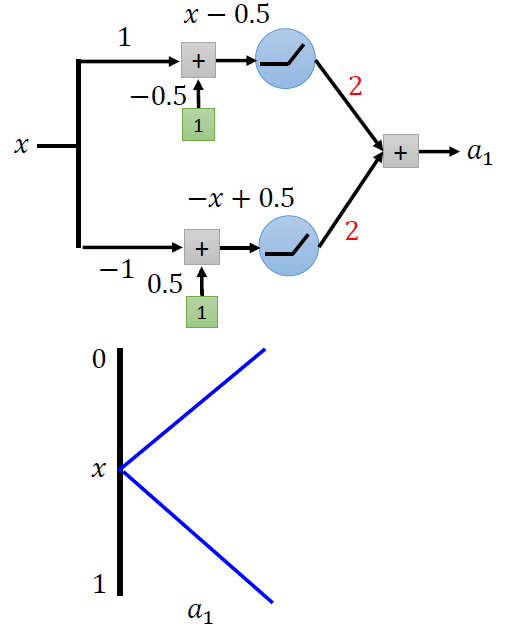
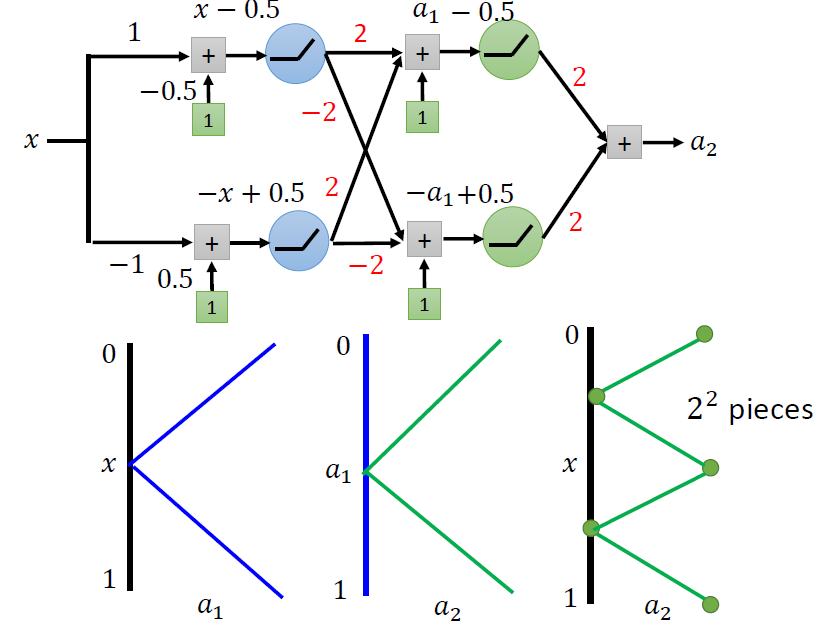
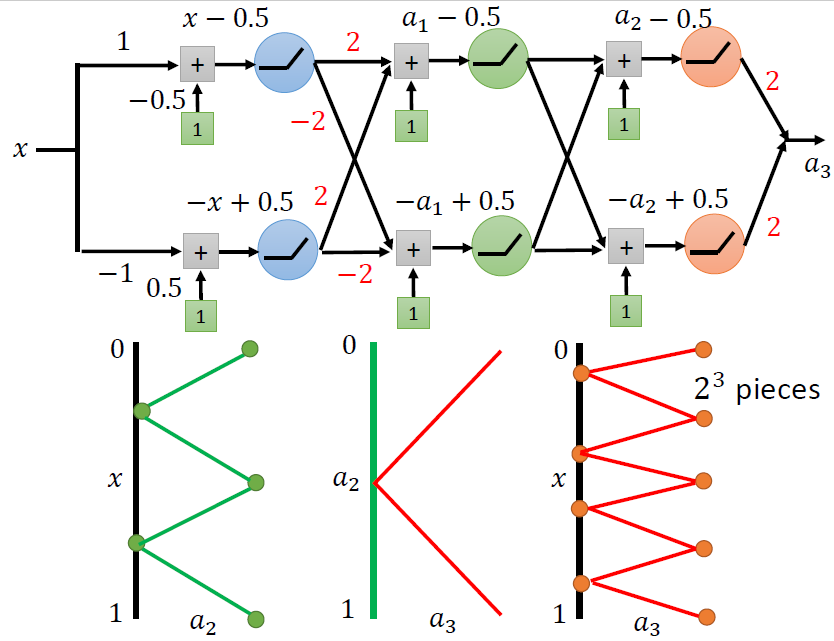
深度和宽度的对比