李宏毅深度学习L1
机器学习
基本任务
Regression
- 回归,预测一个值,期望其与实际值相等
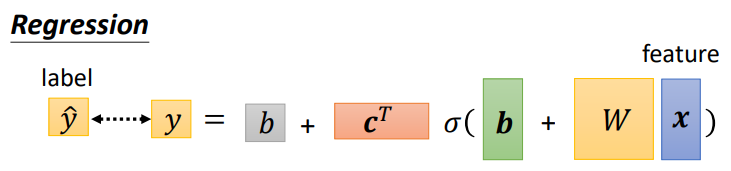
- 损失函数一般使用平均方差(Mean Square Error)
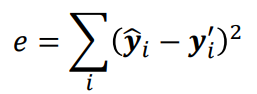
Classification
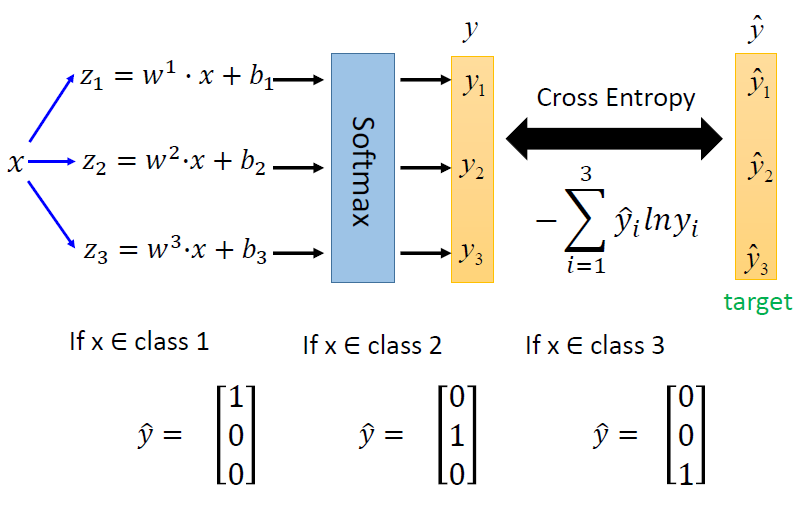
- 分类,输出多个概率值,判断输入属于哪一个类别
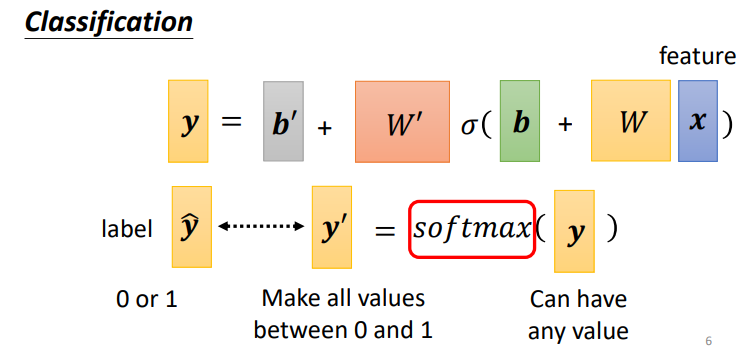
输出值可使用Soft-max将其转换为概率值
classfication的损失函数使用交叉熵(Cross-entropy)
- 交叉熵可以很好地衡量两个概率值之间的差异
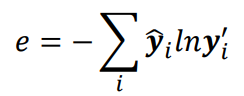
一些概念
Soft-max
- 将多个Classification的多个输出值转换为概率值
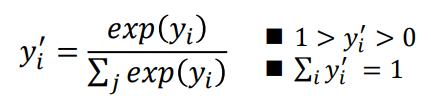
激活函数(Activation function)
Sigmoid
函数: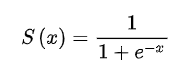
导数:
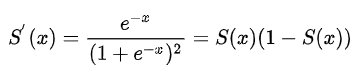
图像:
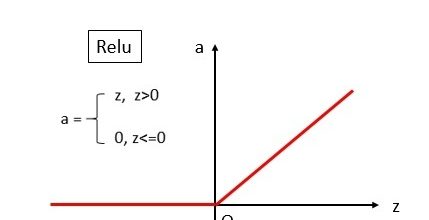
ReLU
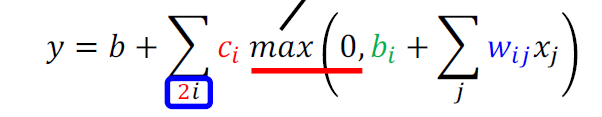
函数: \[ f(X) = max(0,X) \] 图像:
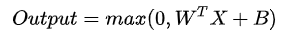
基本步骤
Function(Model) with unknown
函数的集合
Define loss from training data
计算一个函数得到的输出与预期值的差距
输入:一个函数(参数)
输出:函数的优劣程度

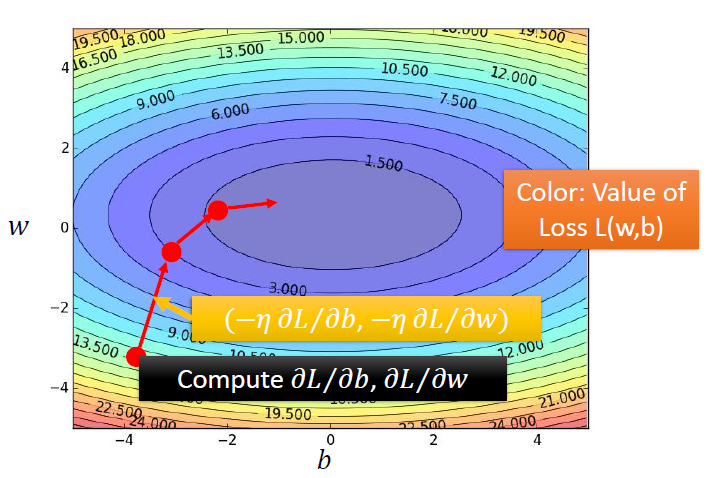
Error surface
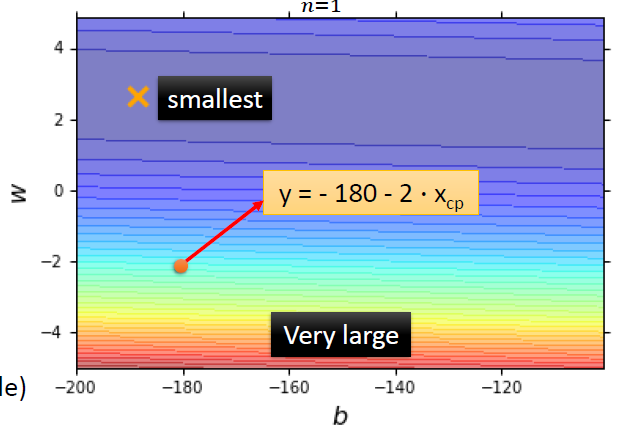
图中的每一个点都是一个函数,颜色代表L(w,b)的大小
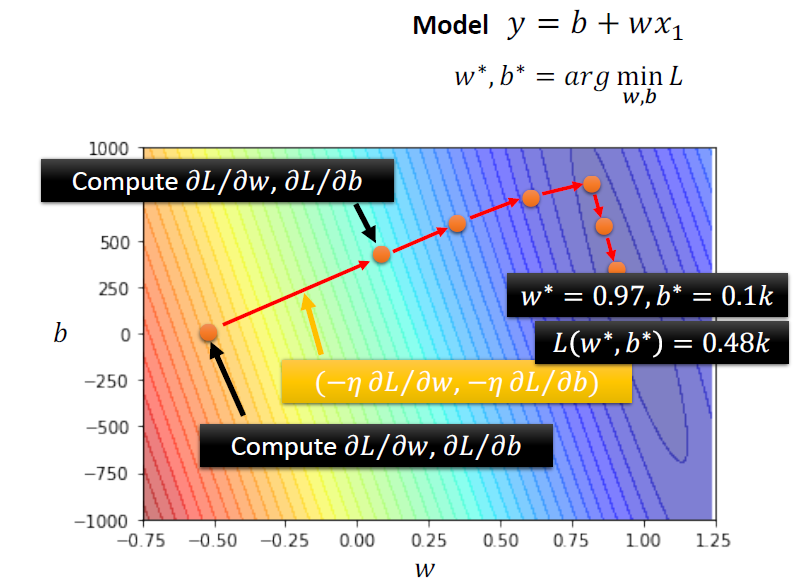
Optimization
可以通过梯度下降来寻找使损失函数变得最小的参数w,b

一些概念
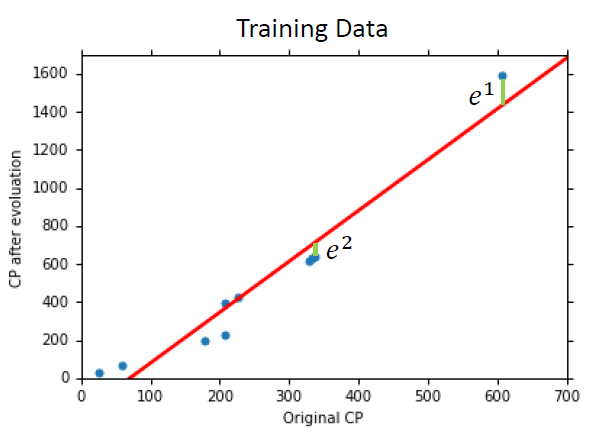
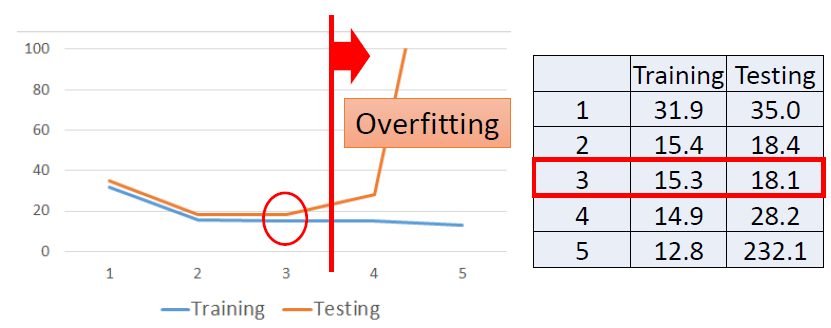
Generalization 一般化
我们真正关心的是模型在新数据(testing data)上的错误率
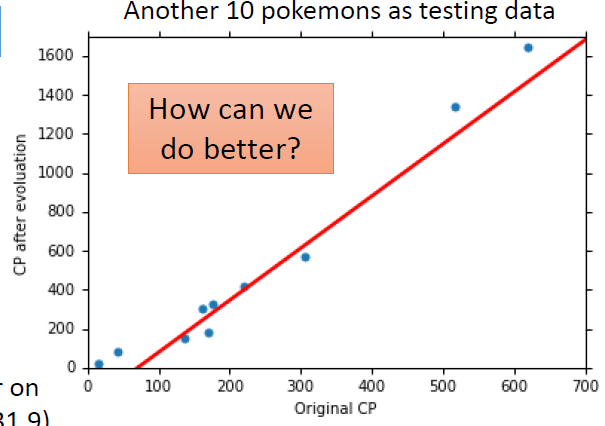
使用更加复杂的模型
使用更加复杂的模型会使我们在训练的数据上表现的更好

但是这往往会造成在测试集数据上过拟合(overfitting)
使用Sigmoid函数构建非线性模型
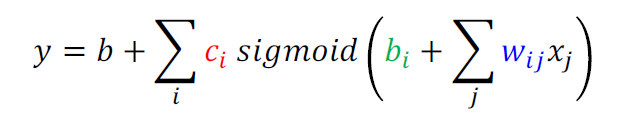
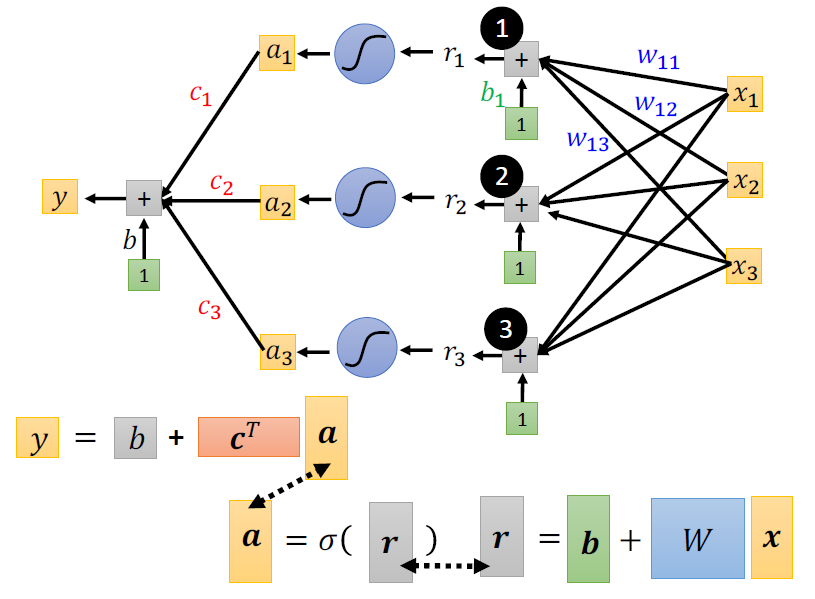
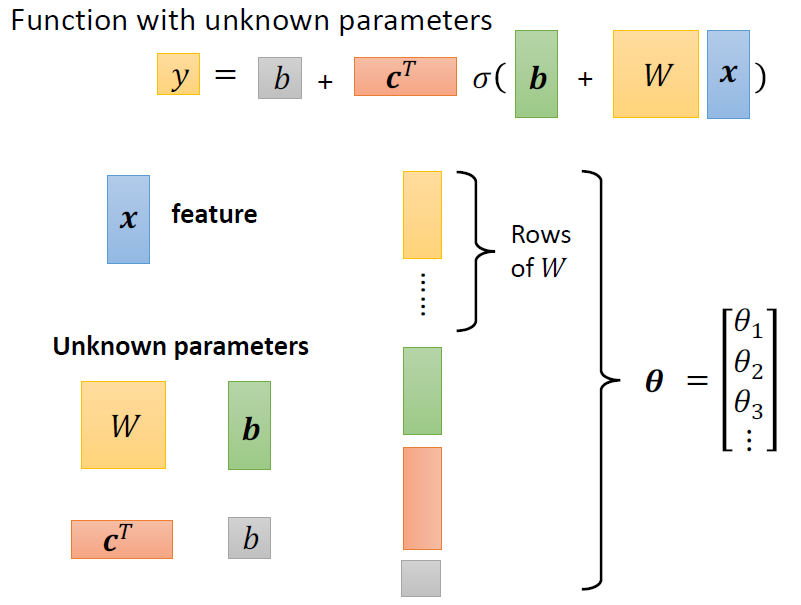
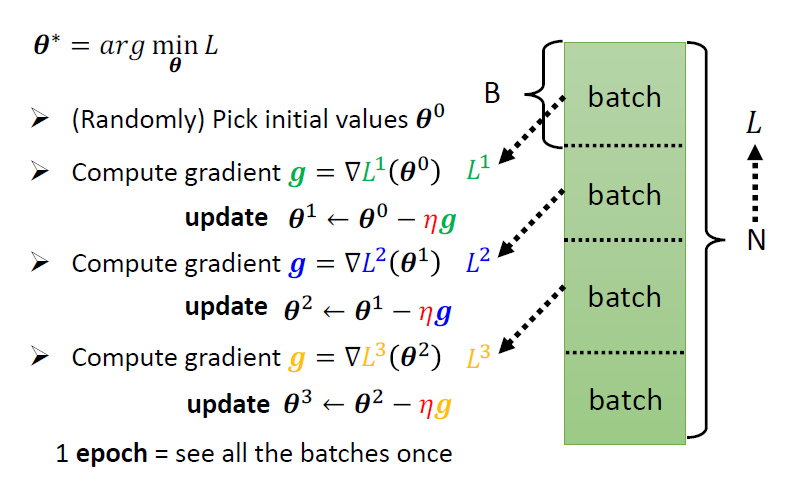
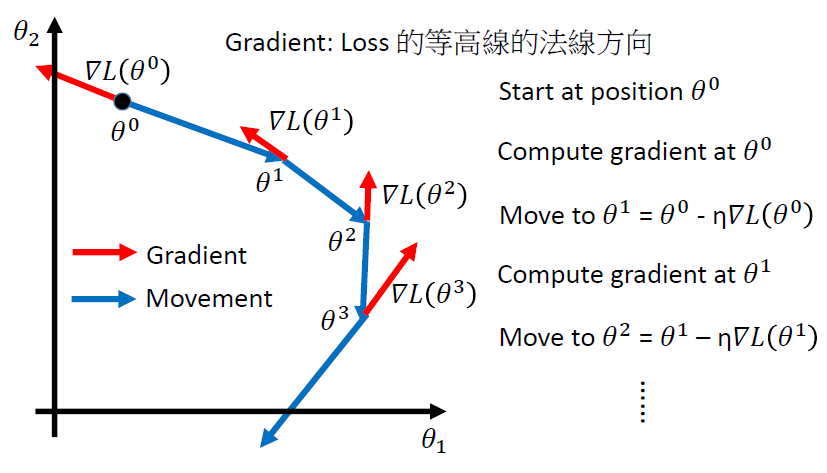
Gradient Descent
\[ \theta^* = arg \mathop{min}{\theta}L(\theta) \]
考虑一个参数w
$$ \[\begin{equation} w^* = arg\mathop{\min}_{\theta}L(w) \end{equation}\] $$
步骤:
- 随机选取一个初始值\(w^0\)
- 计算梯度(导数)\(\frac{dL}{dw}|_{w=w0}\)
- 如果为负,增加w
- 如果为正,减少w
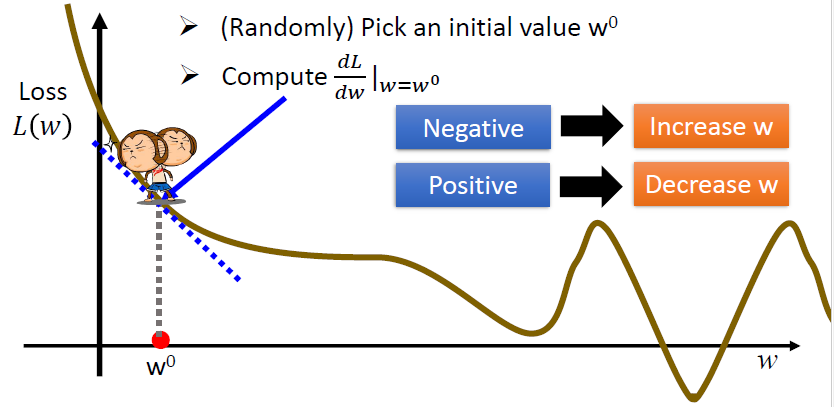
- 更新参数:
\[ w^1 \leftarrow w^0 - \eta\frac{dL}{dw}|_{w=w0} \]
这里的\(\eta\)称为学习率(learning rate)
考虑两个参数w和b
\[ w^*, b^* = arg \mathop{min}_{w, b}L(w, b) \]
它们的梯度:
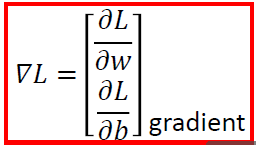
步骤:
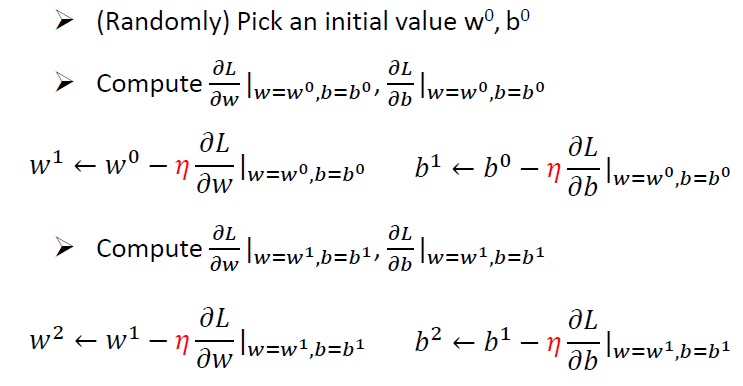
在线性回归模型中,损失函数是凹的,没有局部最优点
求梯度 \[ L(w, b)=\sum^{10}_{n=1} (\hat{y}^n-(b+w *x^n_{cp}))^2 \]
\[ \frac{\partial L}{\partial w} = \sum^{10}_{n=1}2(\hat y^n-(b+w*x^n_{cp}))(-x^n_{cp}) \]
\[ \frac{\partial L}{\partial w} = \sum^{10}_{n=1}2(\hat y^n-(b+w*x^n_{cp})) \]
Learning Rate 学习率
- 步子太大的话容易错过最优点
- 步子太小速度太慢
Adaptive Learning Rates 可调整的学习率
- 基本思想:在每一个epoch中通过一些因素来减小学习率
- 一开始,我们离目标很远,所以要使用较大的学习率
- 在几个epoch之后,我们接近了目标,所以减少学习率
- 学习率不可能是one-size-fits-all
- 给了不同的参数,应该有不同的学习率
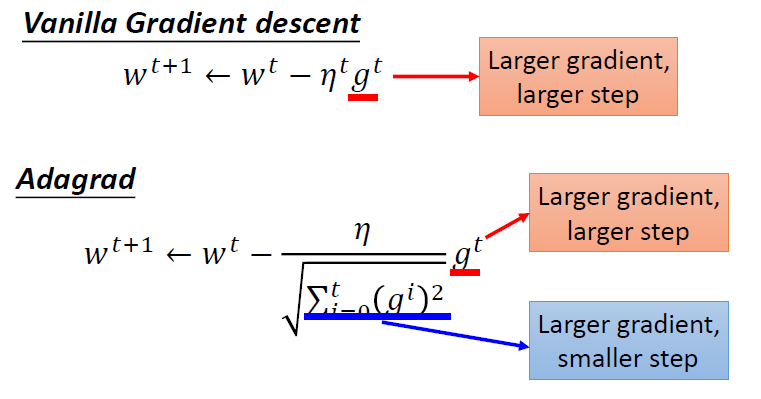
Vanilla Gradient descent
\[ \eta^t=\frac{\eta}{\sqrt{t+1}} \\ g^t=\frac{\partial L(\theta^t)}{\partial w} \\ w^{t+1} \leftarrow w^t - \eta^tg^t \]
Adagrad
使用了root mean square
- 将每个参数的学习率除以其先前导数的均方根(\(\sigma^t\))
\[ \eta^t=\frac{\eta}{\sqrt{t+1}} \\ g^t=\frac{\partial L(\theta^t)}{\partial w} \\ \sigma^t = \sqrt{\frac{1}{t+1}\sum^t_{i=0}(g^i)^2} \\ w^{t+1} \leftarrow w^t - \frac{\eta^t}{\sigma^t}g^t \\ \]
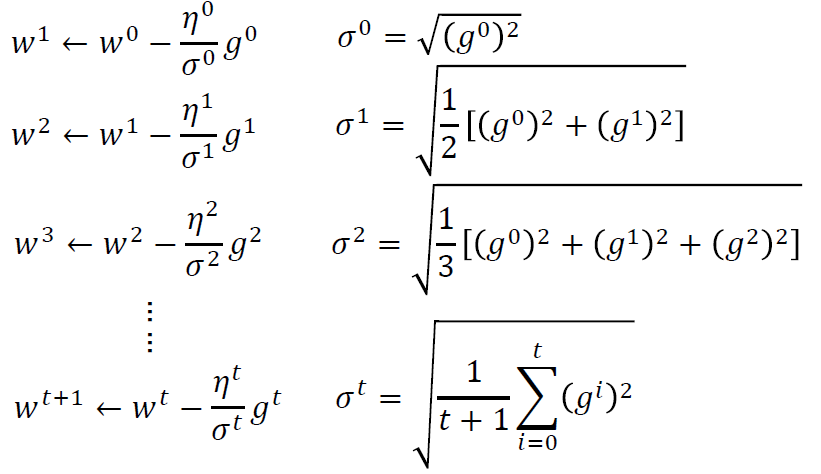
化简
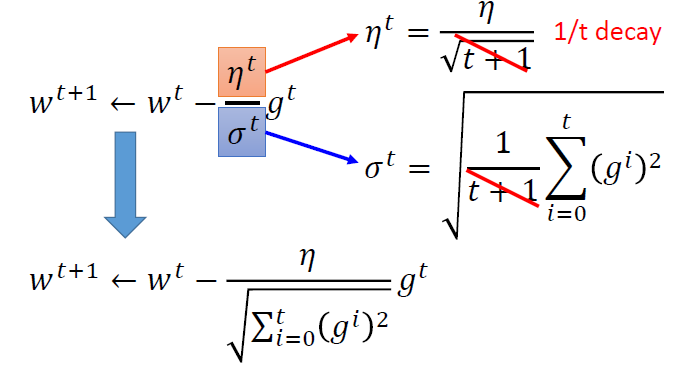
分子与分母作用相反,越大的梯度,我们应该走更大的步才对
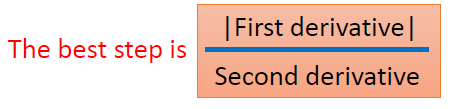
最佳的步骤
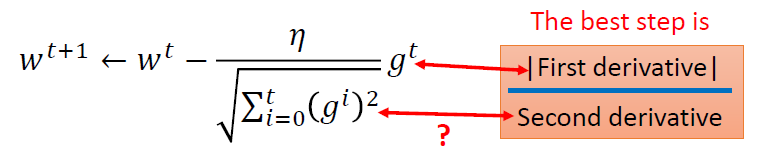
Adagrad是在尝试用一阶导去估计二阶导
Backpropagation
参数\(\theta = {w_1, w_2, \dots, b_1, b_2, \dots}\),不断进行更新

链式法则
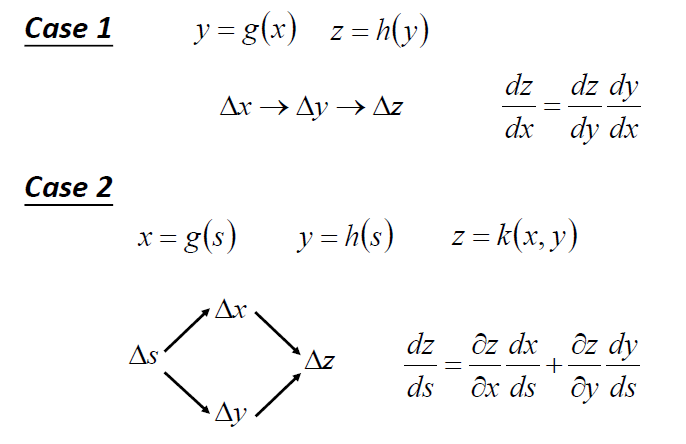
向前传递
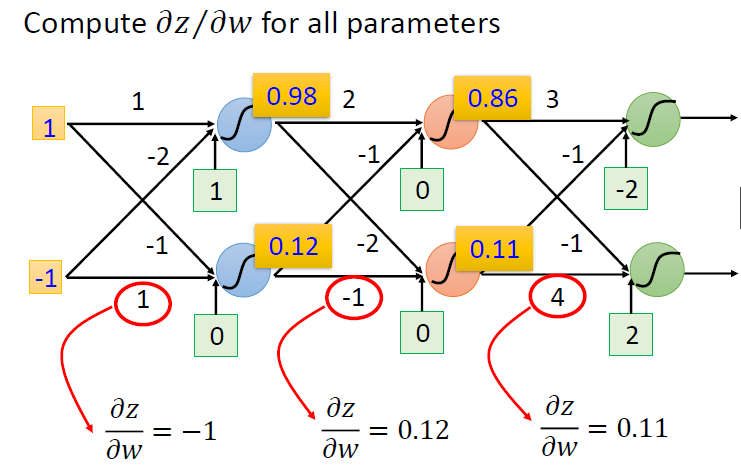
向后传递
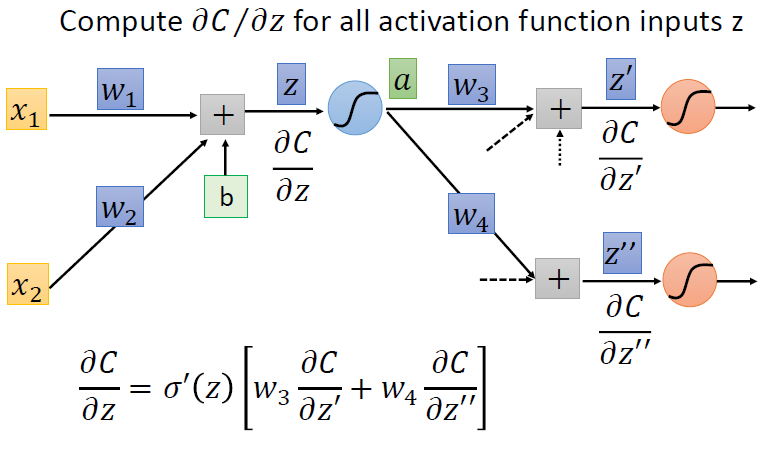 \[
\frac{\partial{C}}{\partial{z}} =
\frac{\partial{a}}{\partial{z}}\frac{\partial{C}}{\partial{a}} \\ \\
\frac{\partial{C}}{\partial{a}} =
\frac{\partial{z^`}}{\partial{a}}\frac{\partial{C}}{\partial{z^`}}+
\frac{\partial{z^{``}}}{\partial{a}}\frac{\partial{C}}{\partial{z^{``}}}
\\ \\
\frac{\partial{z^`}}{\partial{a}} = w_3 \\
\frac{\partial{z^{``}}}{\partial{a}} = w_4 \\ \\
现在的问题是\frac{\partial{C}}{\partial{z^`}}和\frac{\partial{C}}{\partial{z^{``}}}的取值
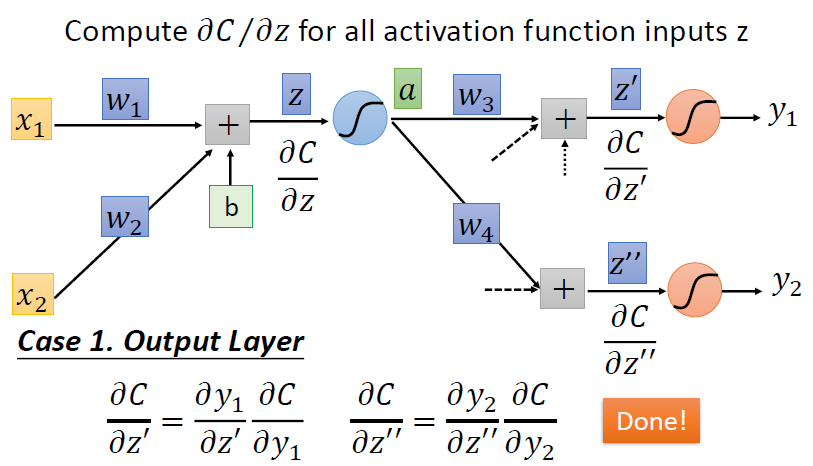
\] 情况一:有输出层
\[
\frac{\partial{C}}{\partial{z}} =
\frac{\partial{a}}{\partial{z}}\frac{\partial{C}}{\partial{a}} \\ \\
\frac{\partial{C}}{\partial{a}} =
\frac{\partial{z^`}}{\partial{a}}\frac{\partial{C}}{\partial{z^`}}+
\frac{\partial{z^{``}}}{\partial{a}}\frac{\partial{C}}{\partial{z^{``}}}
\\ \\
\frac{\partial{z^`}}{\partial{a}} = w_3 \\
\frac{\partial{z^{``}}}{\partial{a}} = w_4 \\ \\
现在的问题是\frac{\partial{C}}{\partial{z^`}}和\frac{\partial{C}}{\partial{z^{``}}}的取值
\] 情况一:有输出层
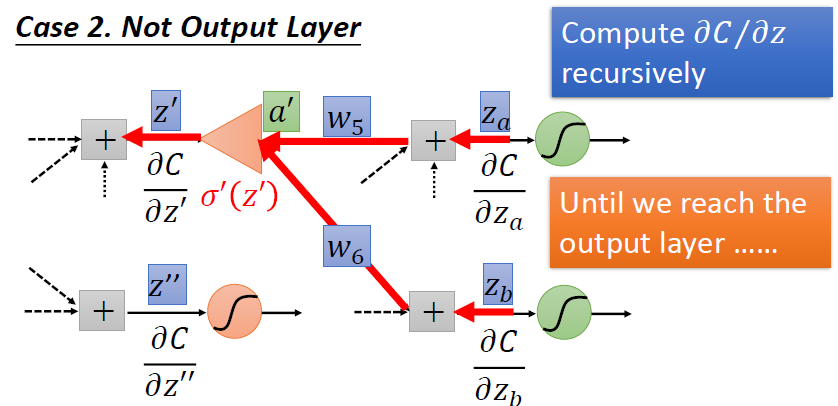
情况二:不是输出层,只是中间层
只能不断地往后算,直到输出层,然后向后传播
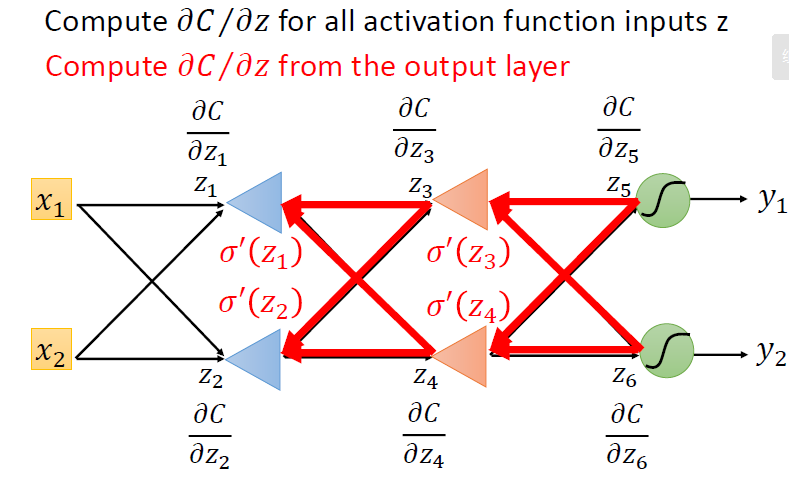
小结
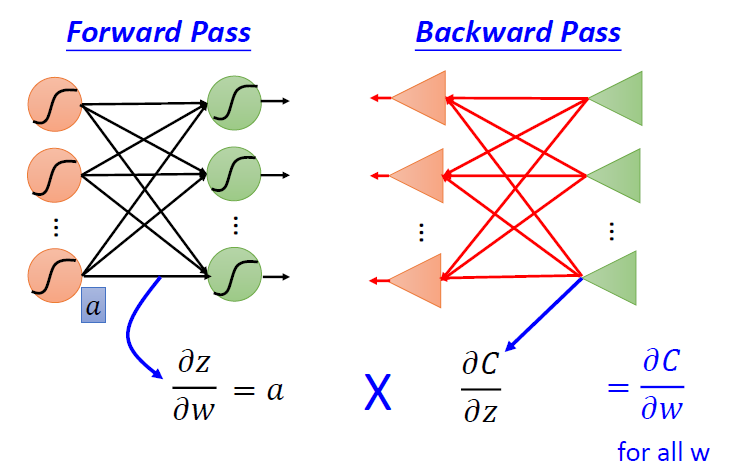 \[
在拥有\frac{\part z}{\part w}和\frac{\part C}{\part
z}的条件下,我们可以通过链式法则得到输出关于参数的梯度\frac{\part
C}{\part w}
\]
\[
在拥有\frac{\part z}{\part w}和\frac{\part C}{\part
z}的条件下,我们可以通过链式法则得到输出关于参数的梯度\frac{\part
C}{\part w}
\]
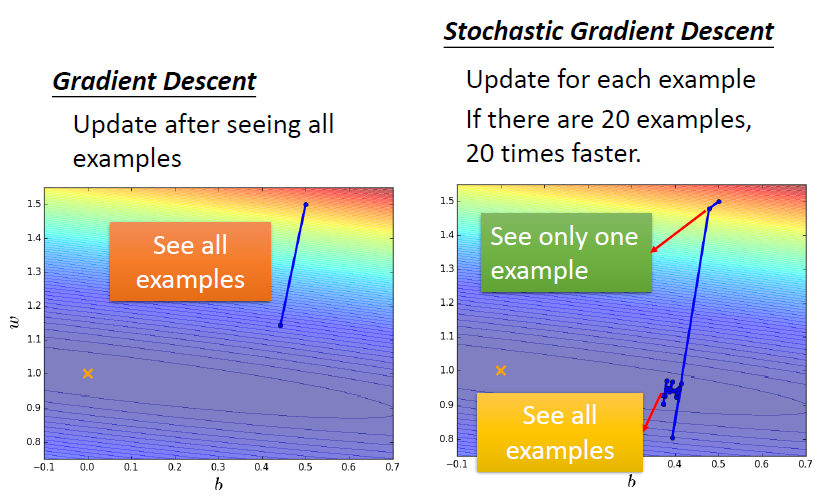
Stochastic Gradient Descent(SGD)
随机梯度下降
对比

在每次更新时用1个样本来计算梯度,然后更新参数
随机也就是说我们用样本中的一个例子来近似我所有的样本,来调整θ
Loss function
L(f) = L(w,b)
- 衡量一组参数的好坏
常用的损失函数
- Mean Square Error(MSE)
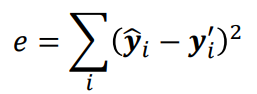
- Cross-entropy
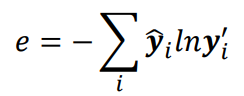
Classification: Probabilistic Generative Model 概率生成模型
分类任务
二元分类问题
给生成模型一个x,模型给出一个类别
Regression
输出1代表类别1,输出-1代表类别2
靠近1代表更大可能属于类别1,反之则是类别二
实际上就是划分出一道线,左边为类别1,右边为类别2
但是如果有一些分布得太远的点,会造成更大的错误
且只能区分两个类别
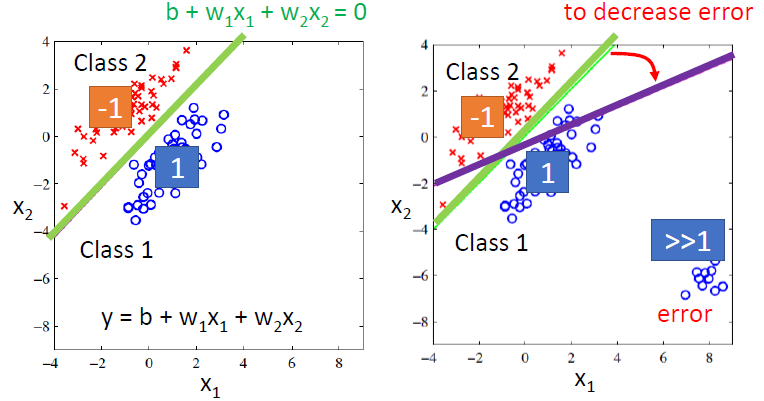
理想的选择

假设两个类别分别为两个箱子
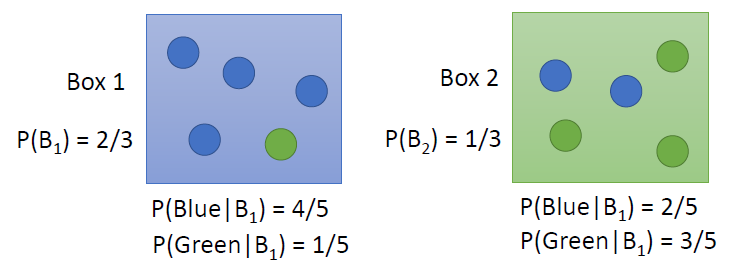
- Box1是类别1,Box2是类别2
- \(P(B_1)\)代表数据集中\(B_1\)占总数的比例,则\(P(B_2)\)代表数据集中\(B_2\)占总数的比例
所以,我们拿到一个蓝色的球,它属于\(B_1\)的概率为
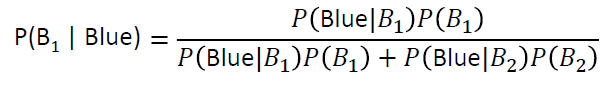
使用高斯分布

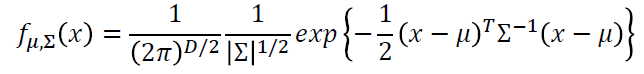
- 输入:向量x
- 输出:采样x的概率
- 方程的形状取决于平均值\(\mu\)和协方差矩阵\(\sum\)
假设我们数据集的点分布符合高斯分布
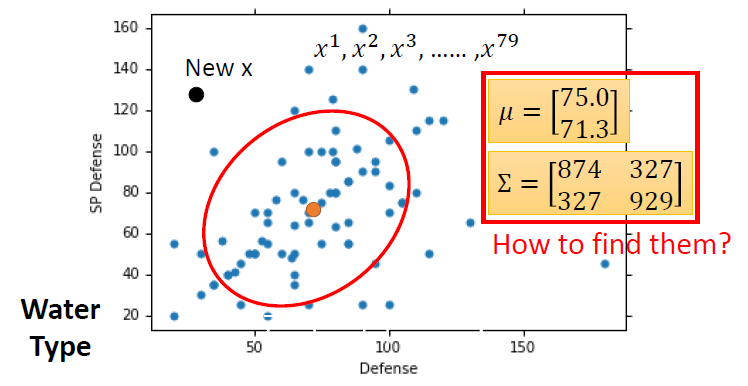
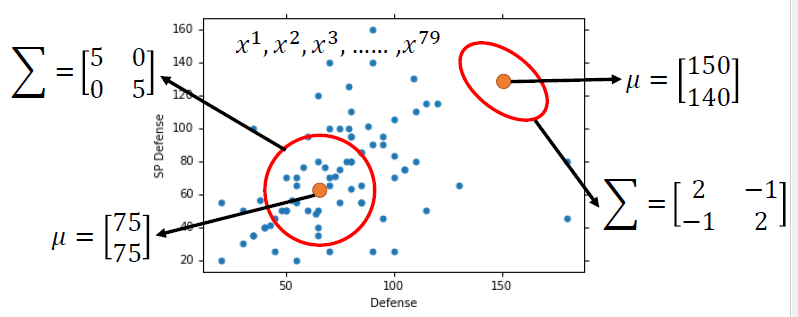
选用不同的平均值和协方差矩阵,会有不同的可能(different likelihood)
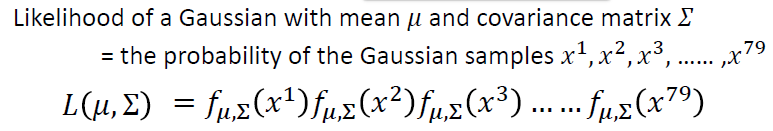
最大似然估计
最大似然原则就是选择使该概率最大的参数
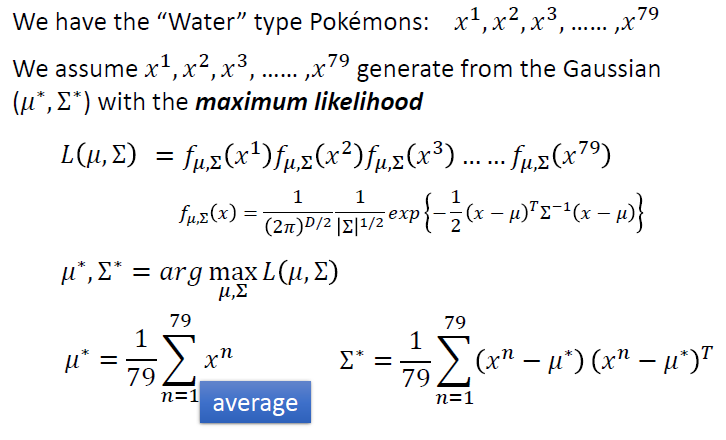
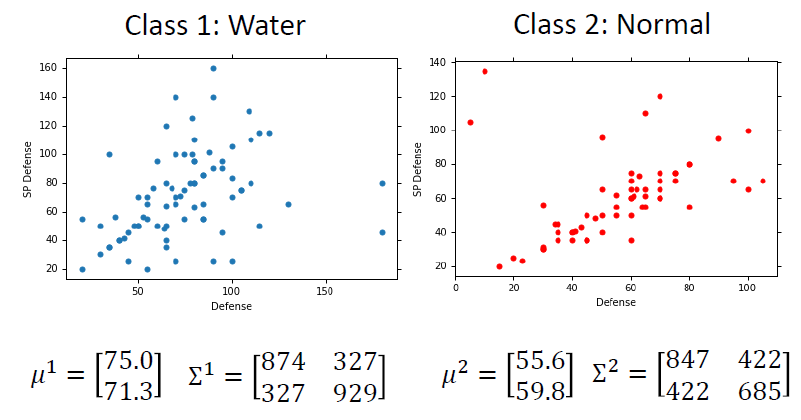
进行分类

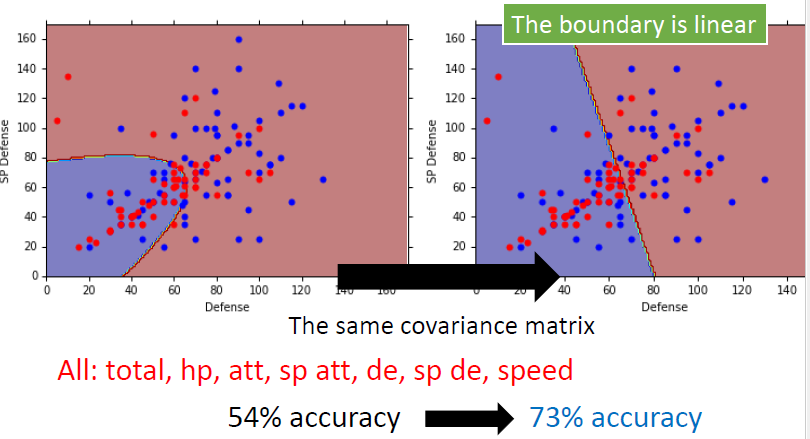
改进
- 使用相同的协方差矩阵
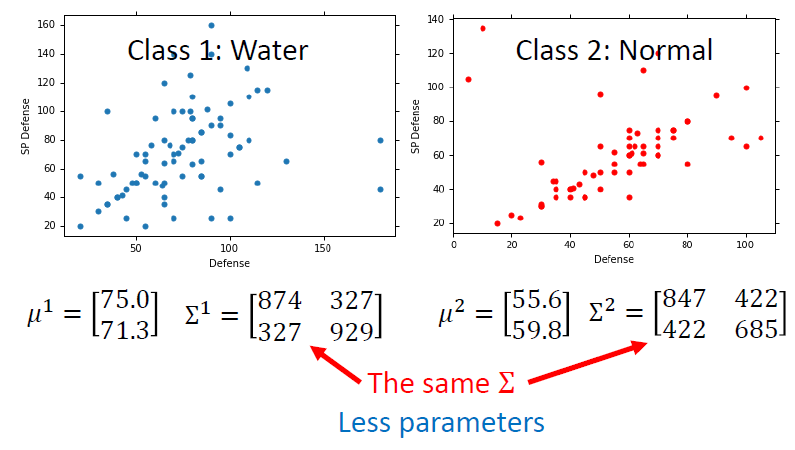

先验概率
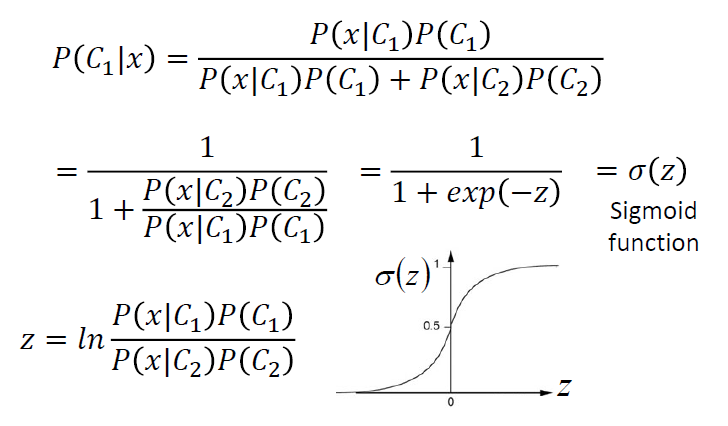

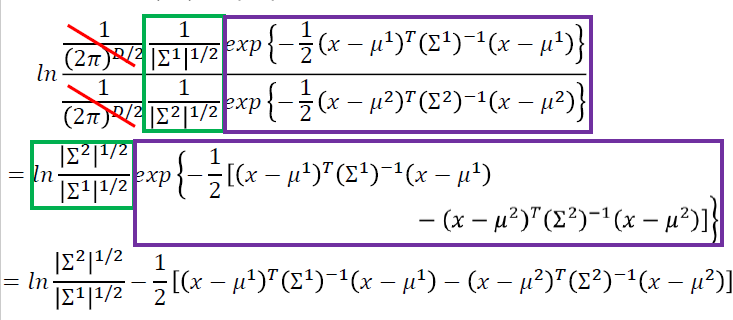
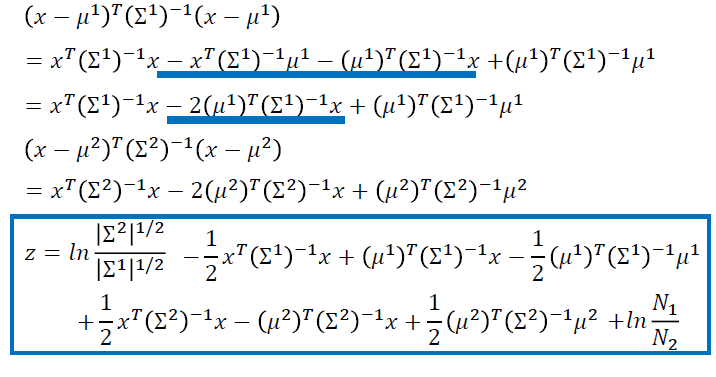

Logistic Regression 逻辑回归
线性的二分类的分类模型
步骤一:函数集(Function Set)
- 函数集:
\[ f_{w,b}(x)=P_{w,b}(C_1|x) \]
- 寻找\(P_{w,b}(C_1|x)\),即拿到x,x属于\(C_1\)的概率
- 如果\(P_{w,b}(C_1|x)\ge0.5\),输出\(C_1\),否则输出\(C_2\)
\[ z = w \cdot x +b \\ P_{w,b}(C_1|x) = \sigma(z) \]
\[ \sigma(z) = \frac{1}{1+exp(-z)} \]
步骤二:函数的优良程度(Goodness of a Function)
我们拥有n个数据集和它们对应的标签
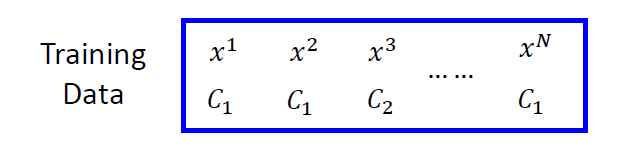
假设数据是根据\(f_{w,b}(x)=P_{w,b}(C_1|x)\)生成的,对应给定的w和b,生成这些数据的概率为 \[ L(w,b) = f_{w,b}(x^1)f_{w,b}(x^2)(1-f_{w,b}(x^3))\cdots f_{w,b}(x^N) \] 根据最大似然估计,最好的参数\(w^*\)和\(b^*\)会使\(L(w,b)\)最大,即 \[ w^*,b^*=arg \mathop{max}_{w,b}L(w,b) \] 为了计算,我们将两个标签$C_1和C_2 $转换为1和0,然后进行最大似然估计
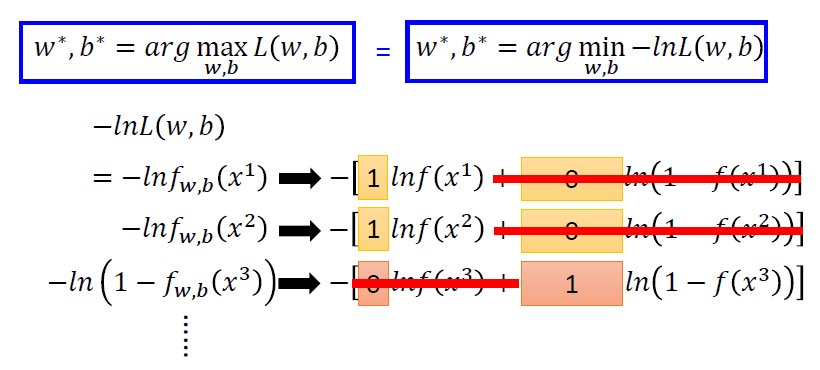
转换为两个伯努利分布的交叉熵

步骤三:找到最好的函数(Find the best function)
求导数
- 第一部分
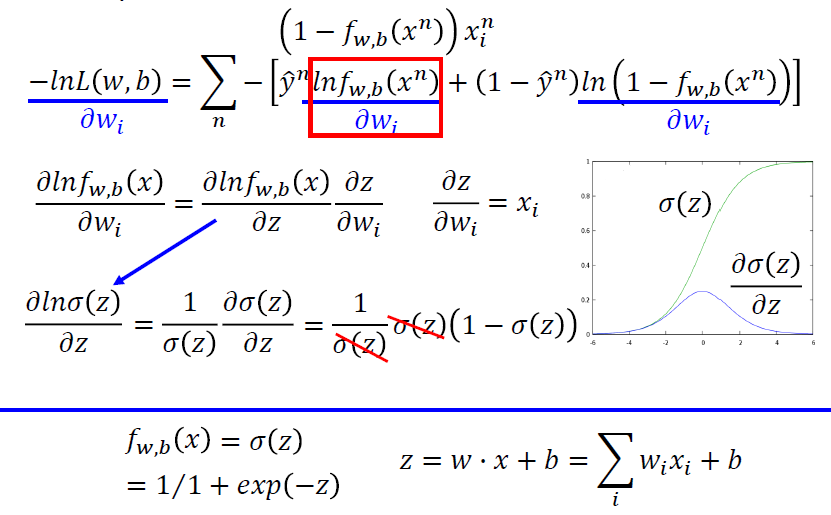
- 第二部分

- 最后的结果

小结

两种方法参数更新的式子是一样的,但是函数的输出和目标不一样
使用不同的损失函数
如果我们使用的损失函数是Square Error

会出现一些问题
- 当我们的输出接近目标时,导数接近0
- 当我们的输出远离目标时,导数接近0
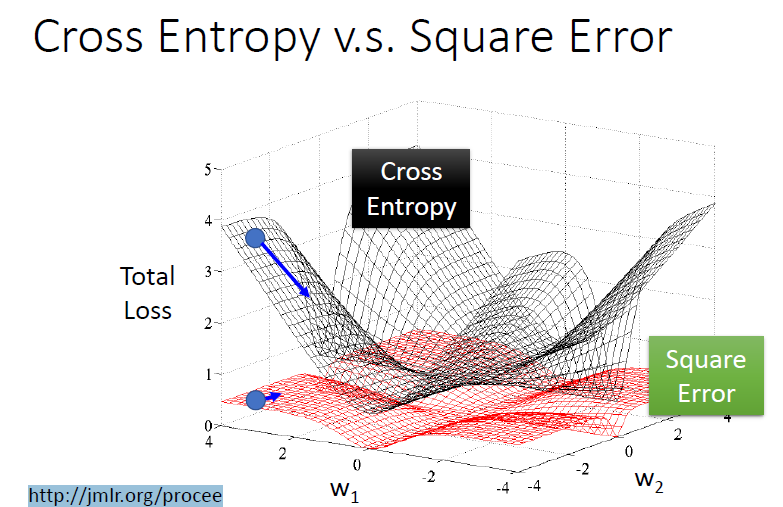
使用Cross Entropy时,我们可以快速地朝目标地方向走,但是Square Error则会比较平坦
离散模型和生成模型的对比
- 离散模型:直接寻找参数w和b
- 生成模型:学习到一个概率分布

相同的函数集,相同的数据集,但是会找到不同的函数
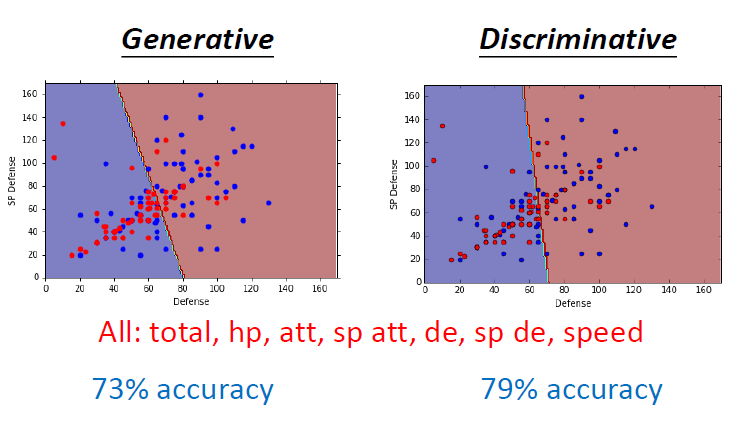
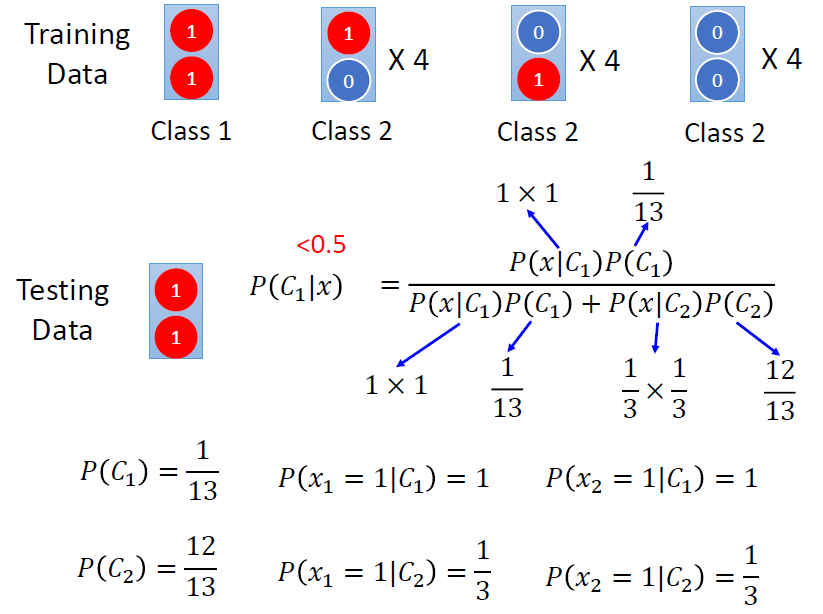
一个例子 使用Naive Bayes
生成模型的优点
- 在概率分布的假设下,需要的训练数据更少
- 在概率分布的假设下,对噪声更鲁棒
- 先验和类依赖概率可以从不同的来源估计
多分类
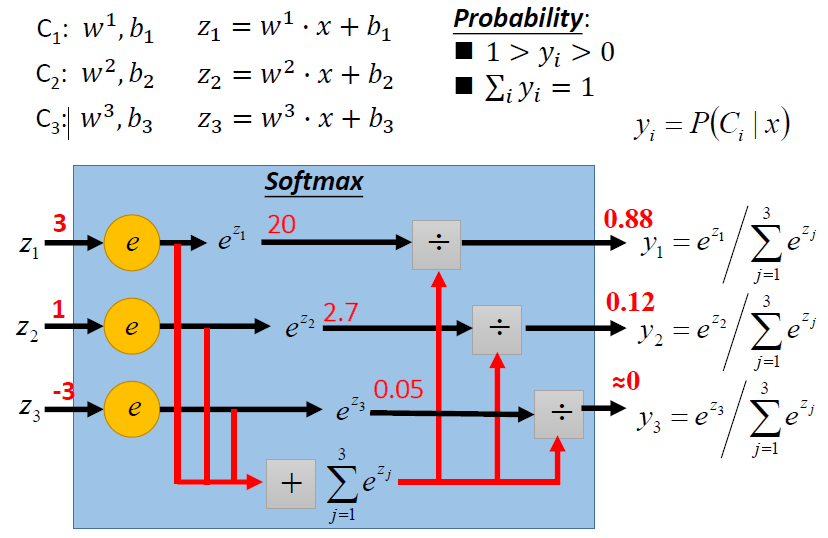
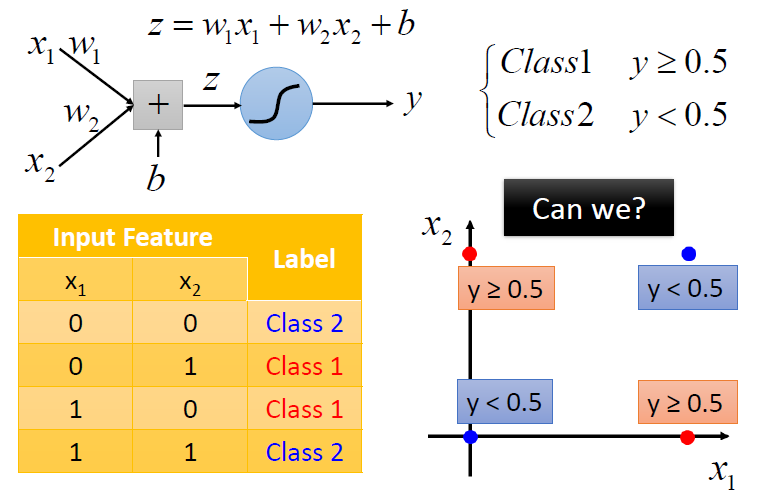
逻辑回归的局限性
逻辑回归是线性的分类模型
深度学习
基本步骤
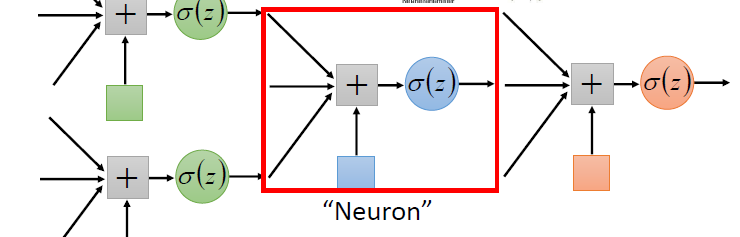
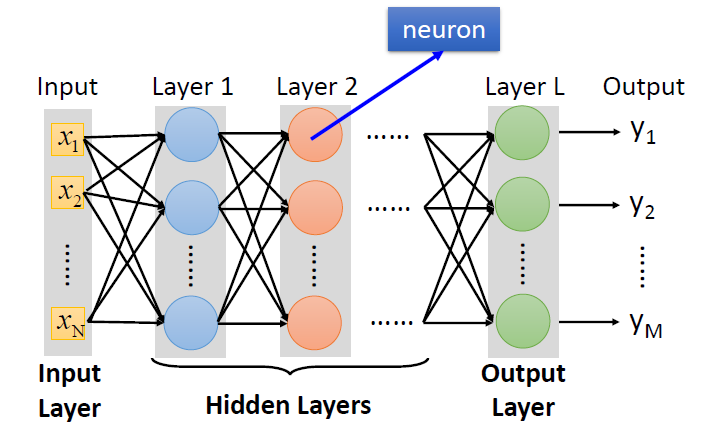
Neural Network
- 不同的联系会指向不同的网络结构
- 网络的参数\(\theta\):神经元中所有的权重(weights)和偏差(biases)
- 给定网络结构,定义一个函数集
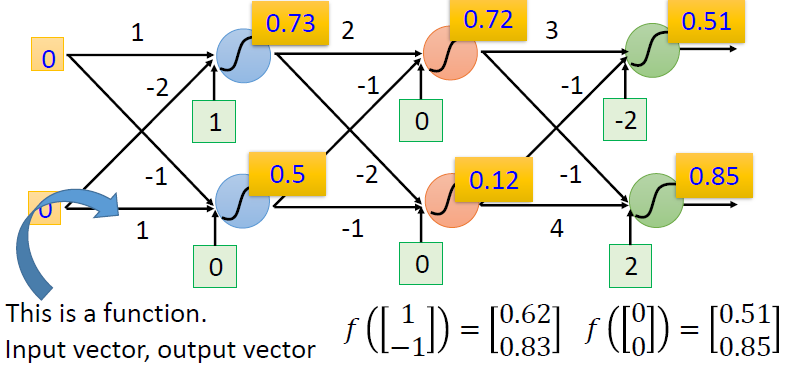
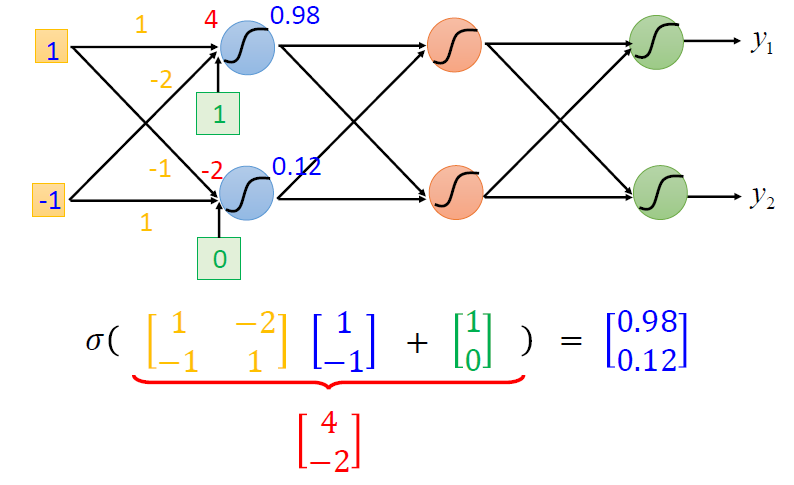
矩阵的操作
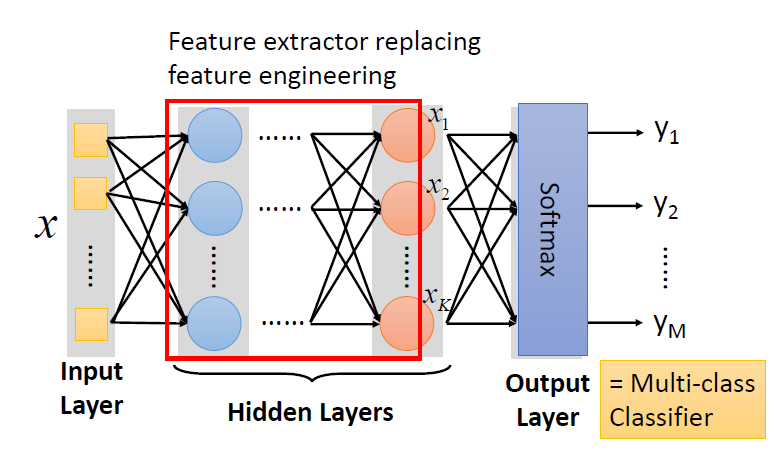
输出层
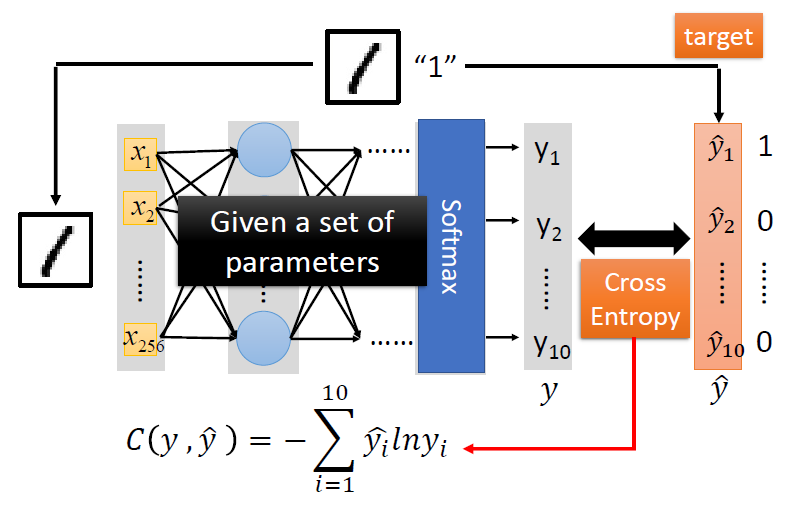
goodness of function
- 定义一个损失函数,找到一个函数,能够使损失函数的值最小化,起始也就是找到合适的参数
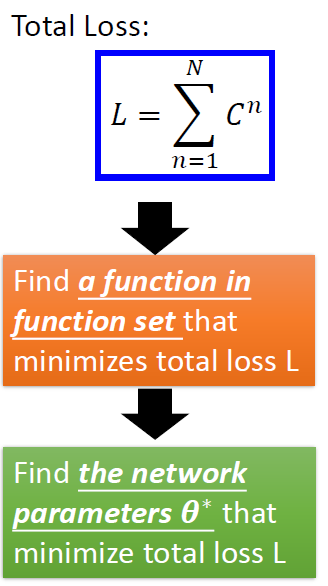
pick the best function
- 使用梯度下降,来寻找能让损失函数降到最小的参数

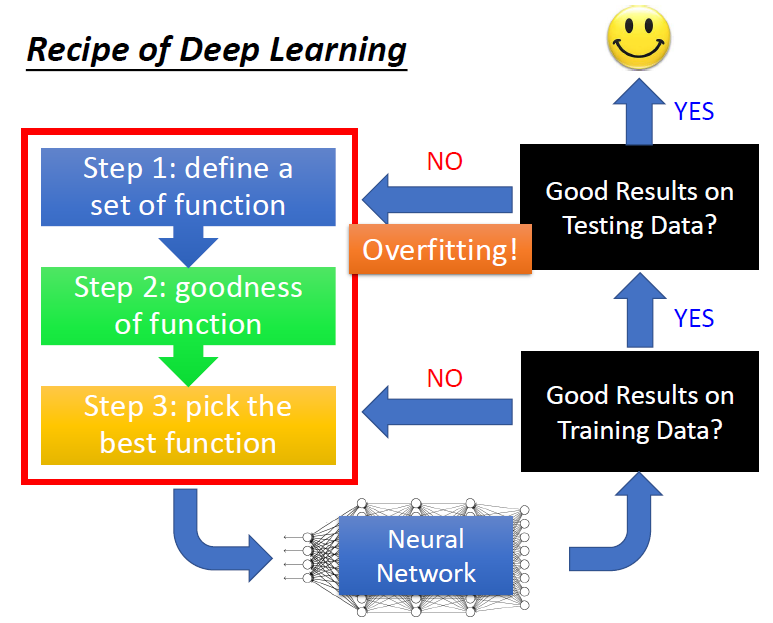
深度学习的一些建议
- 在训练集上表现不好
- 在训练集上表现好,测试集上表现不好
- 可能是Overfitting(过拟合)
各自的解决方法
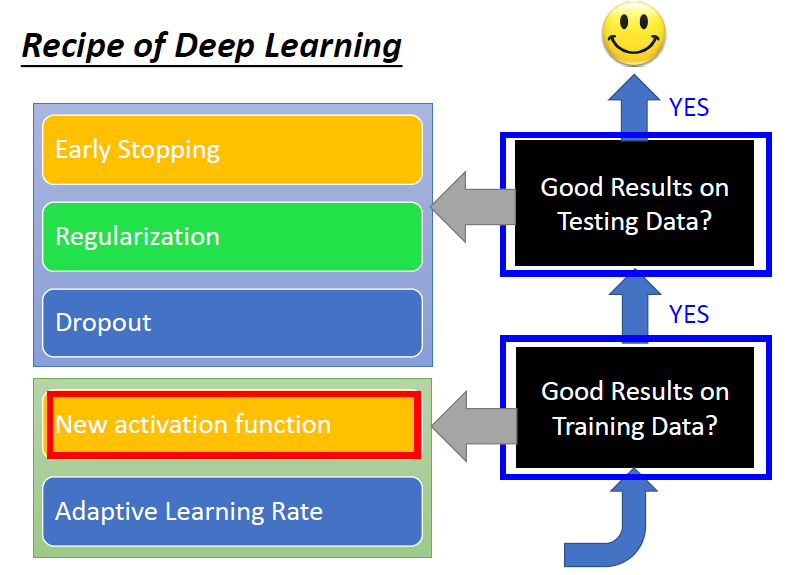
新的激活函数
梯度消失问题
- 浅层的梯度较小,学习非常慢,几乎是随机的
- 与此同时,深层的梯度很大,学习很快,几乎要收敛了
- 这有可能是激活函数的原因,如图
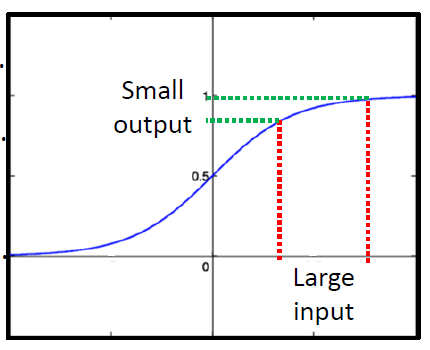
- 因为链式法则不断乘小于1的数,导致梯度非常小的现象
- sigmoid函数的导数,是在0~0.25这个区间的,这意味着,当网络层数越深,那么对于前面几层的梯度,就会非常的小
使用ReLU
ReLU:Rectified Linear Unit
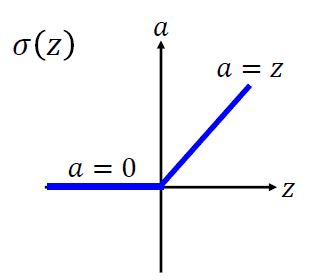
- 优点
- 计算快
- 解决消失梯度问题
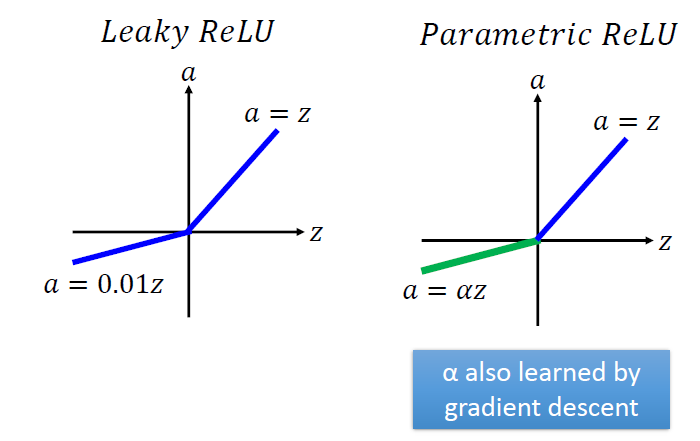
ReLU的变种
- Leaky ReLU
- Parametric ReLU
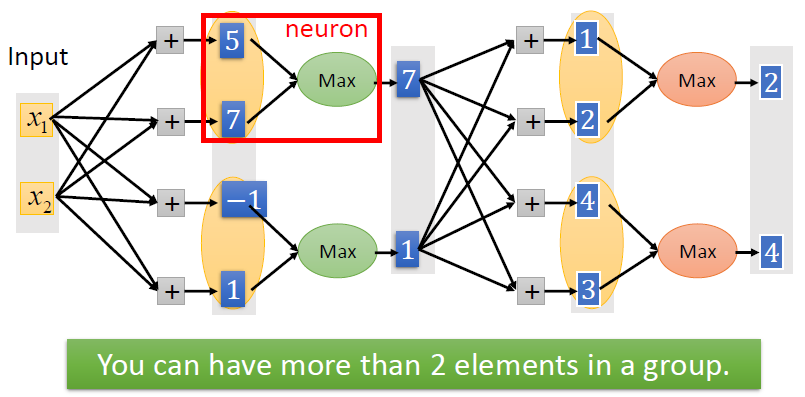
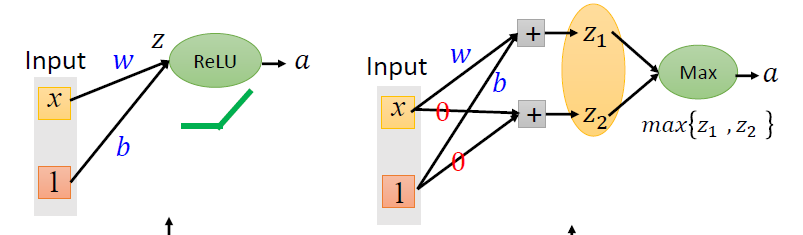
使用Maxout
ReLU是Maxout的一种特殊例子
Adaptive Learning Rate 可调整的学习率
详情见L2
- RMSProp
- Momentum
- Adam
Early stopping
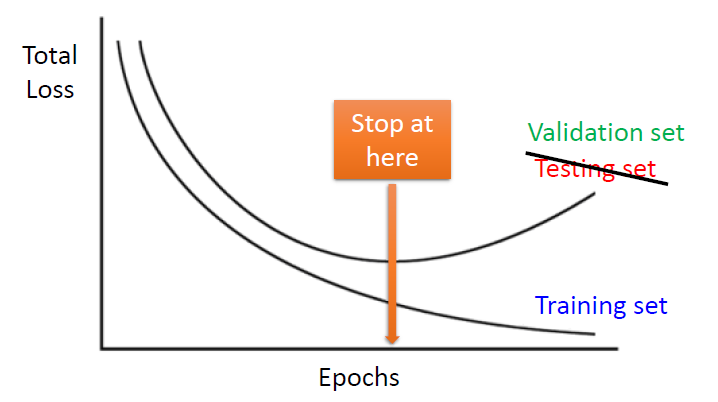
Regularization 正则化
- 对参数进行惩罚--权重衰退
- 防止过拟合
- L2 regularization


- L1 regularization \[ \theta = |w_1| + |w_2| + \dots \]
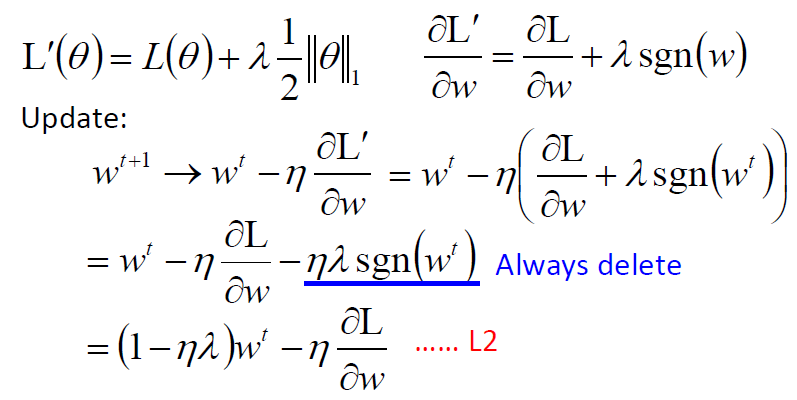
Dropout
- 在每一层丢弃一些神经元
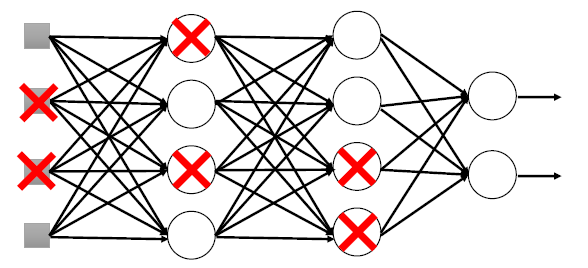
- 改变了网络的结构
pytorch实战部分
数据集
- pytorch中主要使用的是Dataset和DataLoader
1 | from torch.utils.data import Dataset, DataLoader |
- 我们可以构建自己处理数据集的类(继承Dataset)
1 | # 数据集处理及读取 |
- DataLoader可以构建一批一批的数据集合,批量加载数据
1 | # 数据集的批量读取器 |
模型结构
- pytorch中主要使用的是torch.nn
1 | import torch.nn as nn |
- 我们可以构建自己模型结构的类(继承nn.Module)
1 | # 模型结构 |
损失函数
- 使用平均方差
1 | criterion = nn.MSELoss(reduction='mean') |
优化器
- 更新参数
1 | optimizer = torch.optim.SGD(model.parameters(), lr=1e-5, momentum=0.9) |
训练过程
1 | # 训练过程 |
简单的保存数据为csv文件
1 | def save_in_csv(file,res): |