深度学习-2

线性代数

• torch.tensor()
  • 构建张量
  • torch.tensor([3.0])
  • 标量由只有一个元素的张量来表示
• torch.arange()
  • torch.arange(4): tensor([0, 1, 2, 3])
    • 向量可视为标量值组成的列表
  • 用张量的索引访问任一元素
• len(x)：张量的长度
• x.shape：张量的形状
• torch.arange(20).reshape(5, 4)
  • 构建m x n的矩阵
• 矩阵的转置
  • A.T
  • 对称矩阵等于其转置
• torch.arange(24).reshape(2, 3, 4)
  • 更多轴的数据结构
• clone()
  • 克隆
• 哈达玛积：两个矩阵的按元素乘法
  • A * B，两个矩阵中的对应位置的元素相乘
  • 得到的是一个矩阵
• 求和
  • 计算矩阵中元素的和
    • sum()
  • 指定轴进行求和
    • A.sum(axis = 0)
    • A.sum(axis = 1)
    • A.sum(axis = [0, 1])
• 平均值
  • mean()
  • 指定列进行求平均值
    • A.mean(axis = 0)
• 计算总和或均值时保持轴数不变
  • A.sum(axis = 1, keepdims=True)
• 通过广播除法
  • 相同轴数的张量相除
  • A / sum_A
    • sum_A = A.sum(axis = 1, keepdims = True)
• 某个轴计算A元素的累计总和
  • A.cumsum(axis = 0)
• 点积
  • torch.dot(A, B)
  • 相同位置的按元素乘积的和
• 矩阵的向量积
  • torch.mv(A, x)
• 矩阵-矩阵乘法AB
  • torch.mm(A, B)
• 范数
  • L2范数是向量元素平方和的平方根
    • torch.norm()
  • L1范数是向量元素的绝对值之和
    • torch.abs(u).sum()
  • 弗罗贝尼乌斯范数（Frobenius norm） 是矩阵元素平方和的平方根
    • torch.norm(torch.ones((4, 9)))

导数

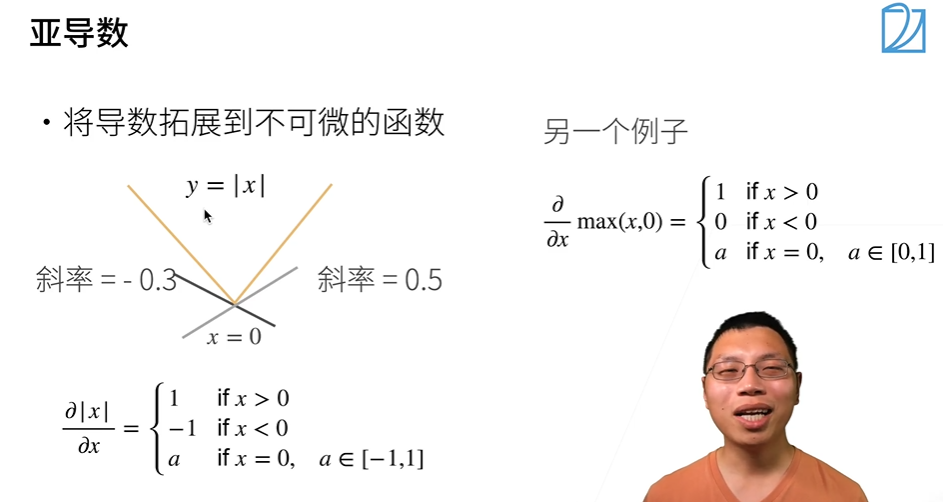
• 导数和亚导数

  • 亚导数：将原函数分段

• 梯度

  • 将导数扩展到向量
  • 粗体是向量，普通为标量

​

​

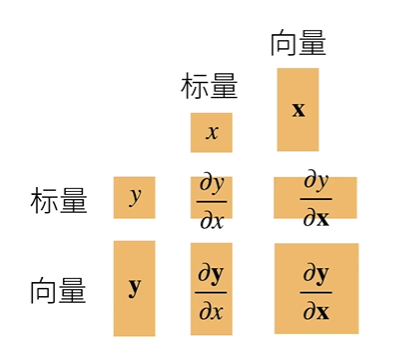
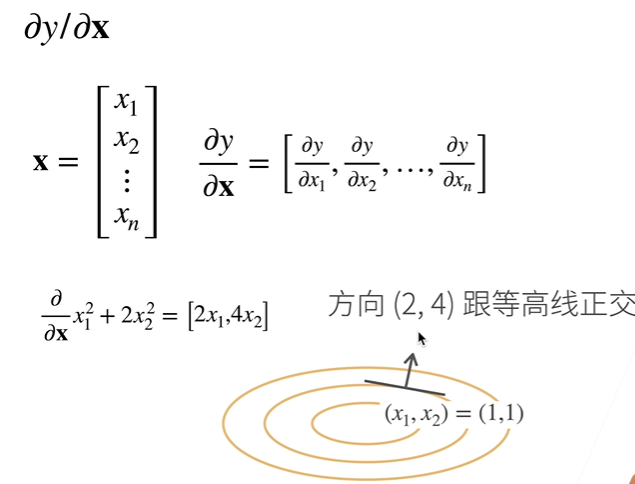
• 样例：

​

​

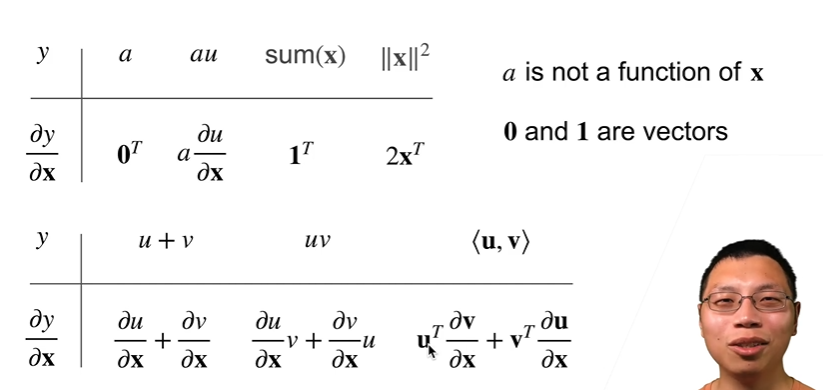
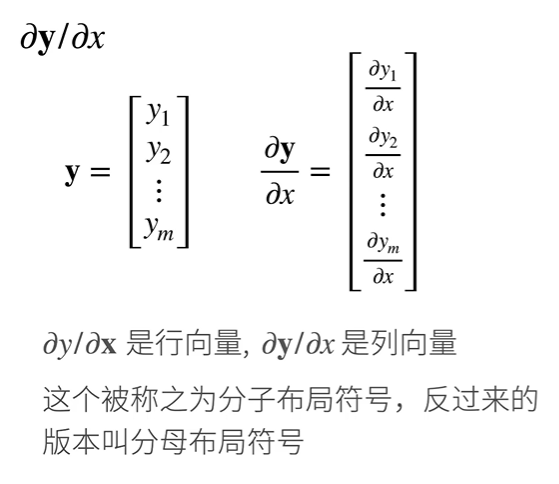
• 扩展到向量对向量的求导

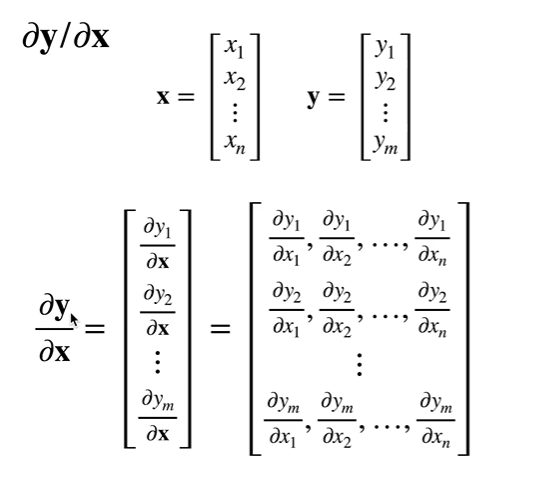
• 样例：

​

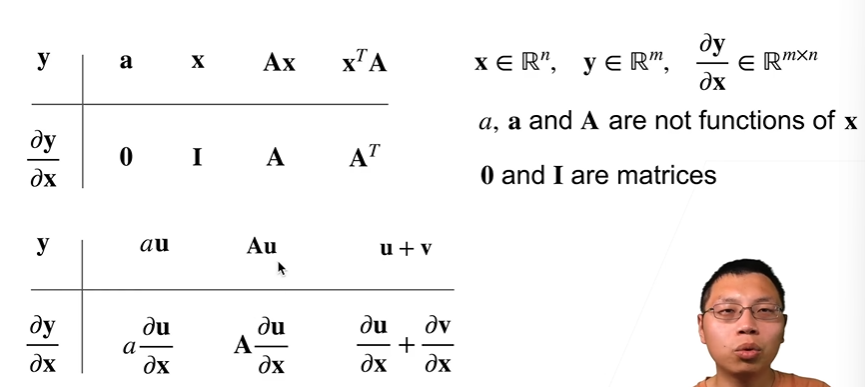
• 扩展到矩阵

​

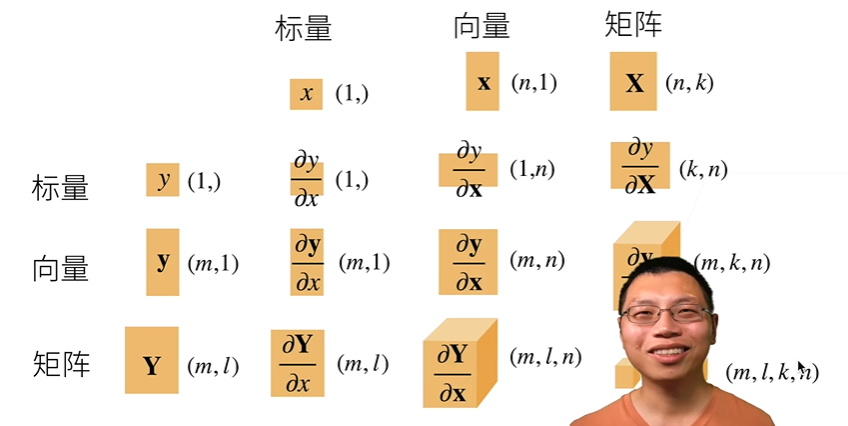
向量的链式法则

​

​

​

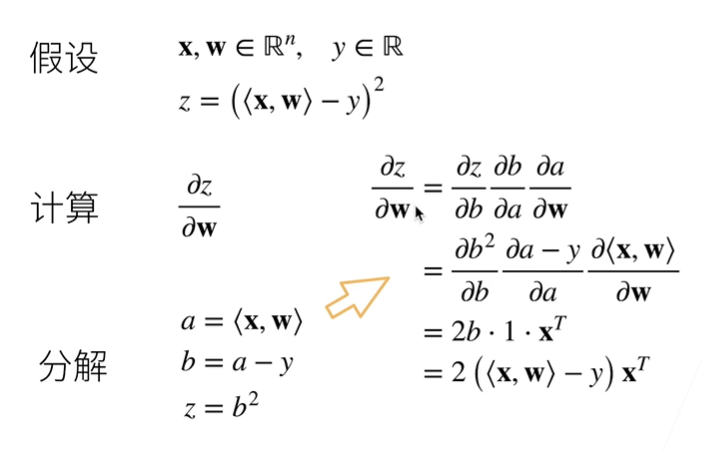
符号求导和数值求导

数值求导：用极限的方法

计算图

​

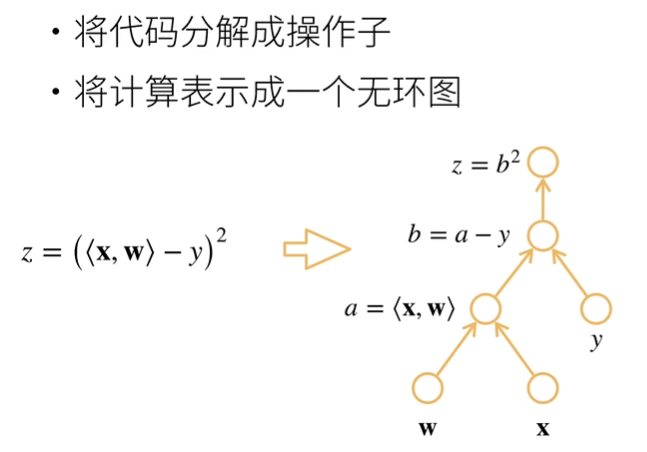
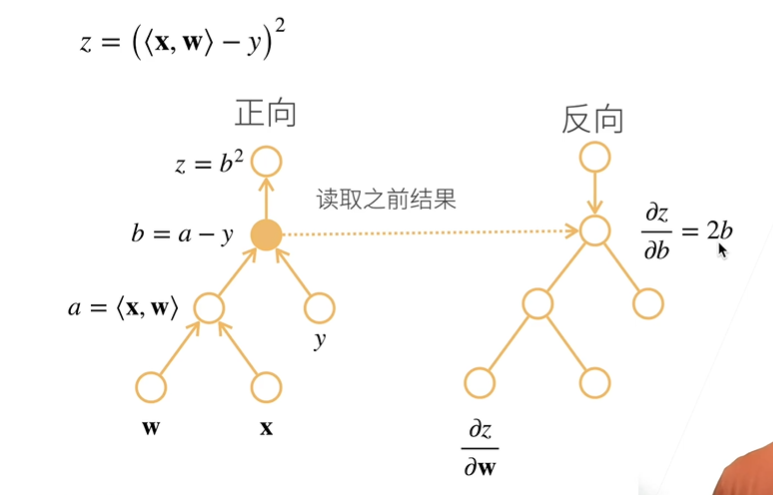
自动求导

• ​ 前向：从最里面的开始求导

• ​ 反向：从最外面的开始求导

  

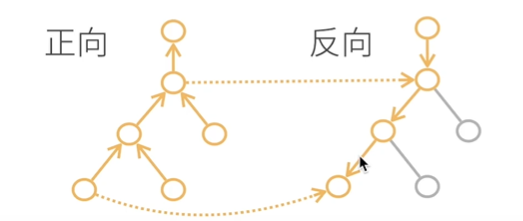
• 总结

  • 前向：执行图，存储中间结果
  • 反向：从相反方向执行图，去除不需要的枝

​

• 复杂度

• 反向：

  • 计算复杂度：O(n)，n是操作子个数
  • 内存复杂度：O(n)，需要存储正向的所有中间结果

• 正向：

• 计算复杂度：O(n)，用来计算一个变量的梯度

• 内存复杂度：O(1)

自动求导的实现

• ​ 存储梯度： x = torch.arange(4.0, requires_grad = True)

• ​ 梯度：x.grad(默认是None)

• ​ 反向传播函数：y.backward()

• ​ 清除之前的梯度：x.grad.zero_()

• ​ y.detach()，将y视为一个常