回归和分类，softmax回归

  • 回归：估计一个连续值
    • 单连续数值输出
    • 自然区间R
    • 跟真实值的区别作为损失
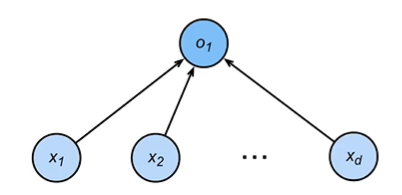
  • 分类：预测一个离散类别
    • 通常多个输出
    • 输出i是预测为第i类的置信度
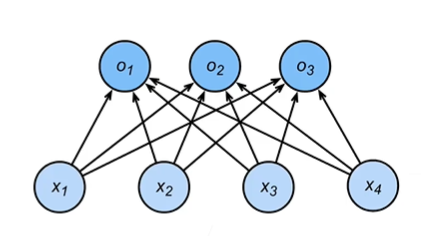
  • 从回归到多类分类
    • 均方损失
      • 对类别进行一位有效编码
        • \(y = [y_1, y_2, y_3, \ldots, y_n]^T\)
        • \(y_i = \begin{cases} 1, & if\quad i = y \\0, & otherwise\end{cases}\)
      • 使用均方损失训练
      • 最大值作为预测
        • \(\hat{y} = argmax{o_i}\)
      • 需要更置信的识别正确类
    • 校验比例
      • 输出匹配概率（非负，和为1）
        • \(\hat{y} = softmax(o)\)
        • \(\hat{y_i} = \frac{exp(o_i)}{\sum_{k} exp(o_k)}\)
      • 概率\(y和\hat{y}\)的区别作为损失
      • 交叉熵
        • 常用来衡量两个概率的区别
          • \(H(p, q) = \sum_i - p_ilog(q_i)\)
        • 将它作为损失
          • \(l(y, \hat{y}) = - \sum_i y_ilog(\hat{y_i})\) = \(-log\hat{y}_y\)
          • 其梯度是真实概率和预测概率的区别
          • \(\partial_{o_i}l(y, \hat{y}) = softmax(o)_i - y_i\)
    • 总结
      • Softmax回归是一个多类分类模型
      • 使用Softmax操作子得到每个类的预测置信度
      • 使用交叉熵来测量预测和标号的区别作为损失函数

损失函数

  • L2 Loss
    • \(l(y, y') = \frac{1}{2}(y - y')^2\)
    • \(y:真实值，y':预测值\)
  • L1 Loss
    • \(l(y, y') = |y - y'|\)
  • Huber's Robust Loss
    • \(l(y, y') = \begin{cases} |y - y'| - \frac{1}{2} & if \quad |y - y'| > 1 \\ \frac{1}{2}(y - y')^2 & otherwise \end{cases}\)

图像分类数据集

  • MNIST数据集是图像分类中广泛使用的数据集之一，过于简单
  • 使用类似但更复杂的Fashion-MNIST数据集
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
import torch
import torchvision
from torch.utils import data
from torchvision import transforms
from d2l import torch as d2l
import os
os.environ["KMP_DUPLICATE_LIB_OK"]="TRUE"
d2l.use_svg_display()

# 通过框架中的内置函数将Fashion-MNIST数据集下载并读取到内存中
# 通过ToTensor实例将图像数据从PIL类型变换成32位浮点数格式
# 并除以255是的所有像素的数据均在0到1之间
trans = transforms.ToTensor()
mnist_train = torchvision.datasets.FashionMNIST(
    root = '../data', train = True, transform = trans, download = False
)
mnist_test = torchvision.datasets.FashionMNIST(
    root = '../data', train = False, transform = trans, download = False
)

def get_fashion_mnist_labels(labels):
    '''返回Fashion-MNIST数据集的文本标签'''
    text_labels = [
        't-shirt', 'trouser', 'pullover', 'dress', 'coat', 'sandal',
        'shirt', 'sneaker', 'bag', 'ankle boot']
    return [text_labels[int(i)] for i in labels]

def show_images(imgs, num_rows, num_cols, titles = None, scale = 1.5):
    figsize = (num_cols * scale, num_rows * scale)
    _, axes = d2l.plt.subplots(num_rows, num_cols, figsize=figsize)
    axes = axes.flatten()
    for i, (ax, img) in enumerate(zip(axes, imgs)):
        if torch.is_tensor(img):
            ax.imshow(img.numpy())
        else:
            ax.imshow(img)

batch_size = 256

def get_dataloader_workers():
    """使用4个进程来读取数据"""
    return 4

# 为了使我们在读取训练集和测试集时更容易，我们使用内置的数据迭代器
# 数据加载器每次都会读取一小批量数据，大小为batch_size。
# 我们在训练数据迭代器中还随机打乱了所有样本。
train_iter = data.DataLoader(mnist_train, batch_size, shuffle=True, 
                            num_workers=get_dataloader_workers())

# 读取训练数据所需的时间
timer = d2l.Timer()
for X, y in train_iter:
    continue
print(f'{timer.stop():.2f} sec')

# 定义 load_data_fashion_mnist 函数 用于获取和读取Fashion-MNIST数据集
# 返回训练集和验证集的数据迭代器
# 还接受一个可选参数，用来将图像大小调整为另一种形状
def load_data_fashion_mnist(batch_size, resize=None):  #@save
    """下载Fashion-MNIST数据集，然后将其加载到内存中。"""
    trans = [transforms.ToTensor()]
    if resize:
        trans.insert(0, transforms.Resize(resize))
    trans = transforms.Compose(trans)
    mnist_train = torchvision.datasets.FashionMNIST(root="../data",
                                                    train=True,
                                                    transform=trans,
                                                    download=False)
    mnist_test = torchvision.datasets.FashionMNIST(root="../data",
                                                   train=False,
                                                   transform=trans,
                                                   download=False)
    return (data.DataLoader(mnist_train, batch_size, shuffle=True,
                            num_workers=get_dataloader_workers()),
            data.DataLoader(mnist_test, batch_size, shuffle=False,
                            num_workers=get_dataloader_workers()))


train_iter, test_iter = load_data_fashion_mnist(32, resize=64)
for X, y in train_iter:
    print(X.shape, X.dtype, y.shape, y.dtype)
    break