李宏毅深度学习L3
Convolutional Neural Network (CNN)
- CNN,即卷积神经网络,主要适用于图片处理
图片分类
- 假设我们现在有一张彩色的图片,在电脑中它有红绿蓝三个通道,每个通道是一个100*100的矩阵
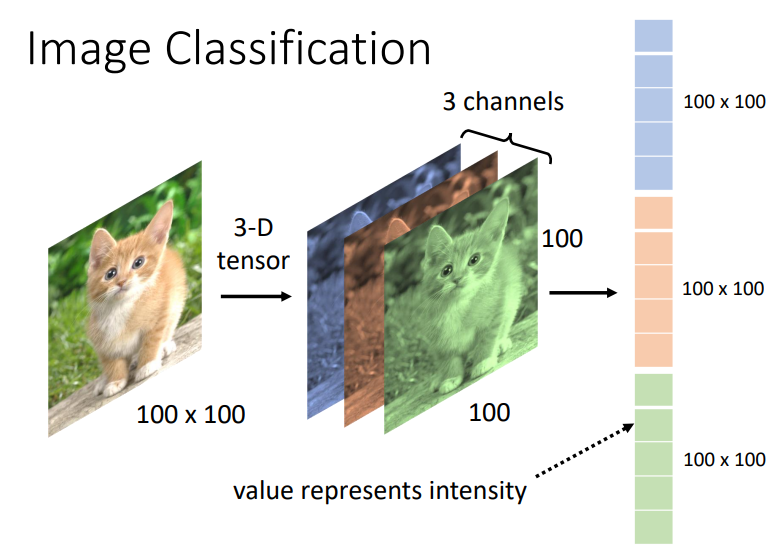
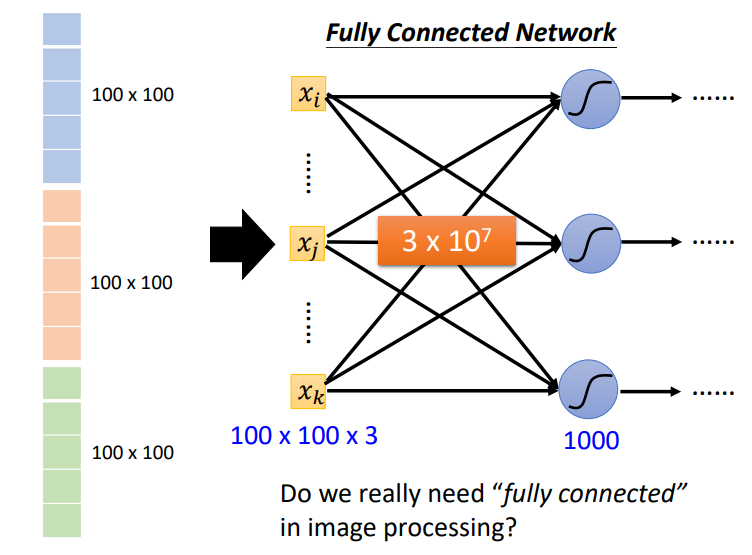
- 但是对于图片来说,如果我们使用全连接层的模型,参数会变得特别多
感受野
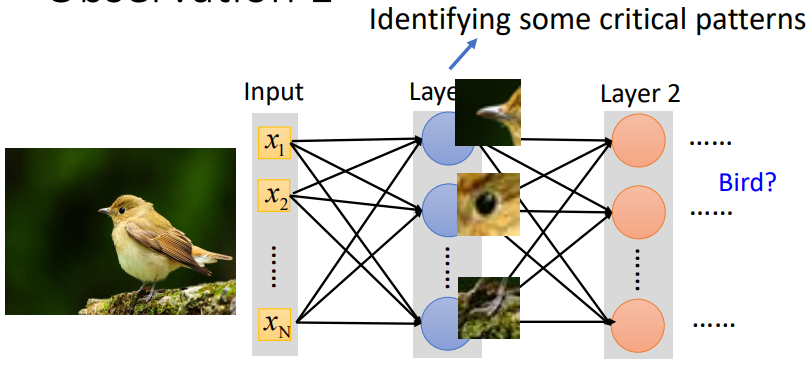
- 我们观察到对于图像分类来说,要抓住的是图像中物体的特征,需要去捕捉图片的局部信息
- 如图中鸟的特征:鸟喙、眼睛、鸟爪
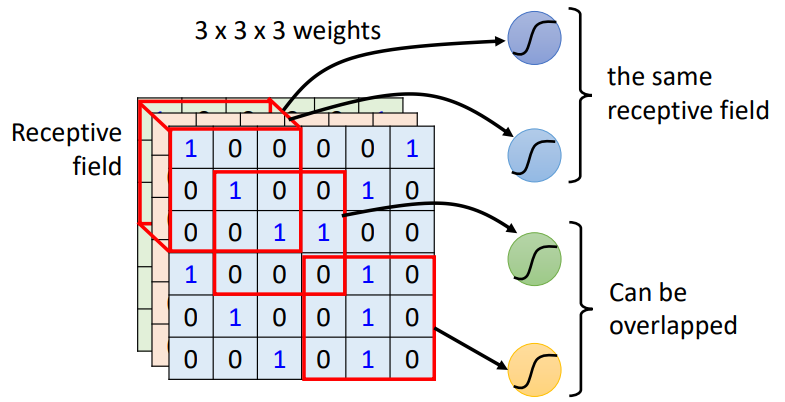
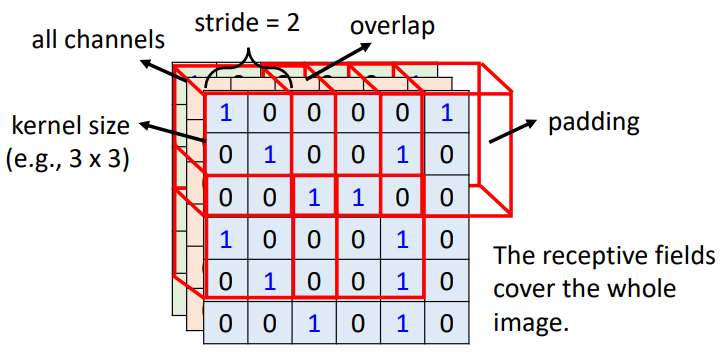
- 所以我们设置一个感受野(Receptive
field)区域,来提取这一区域覆盖的图片信息(局部信息),并将信息给予一个神经元
- kernel size(感受野或者叫卷积核的大小):\(n \times n\),一般为\(3\times3\)
- 区域可以重叠
- stride:移动感受野到图片的下一个区域的跨步
- padding:当感受野来到图片边界,剩下区域不够大时的填充
- 常规设置:每一个感受野有一组神经元(例如64个神经元)
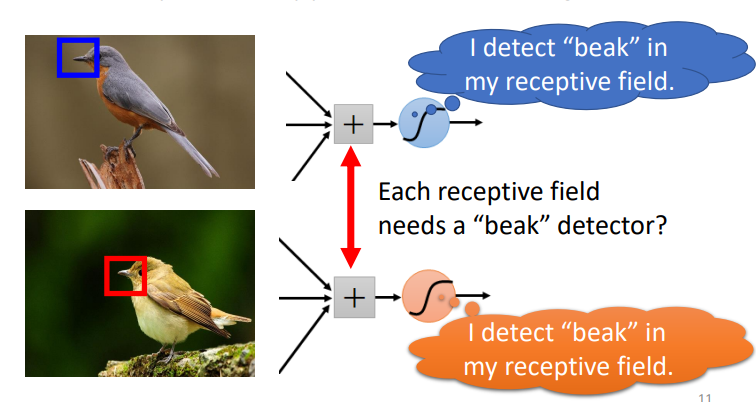
相同特征在不同区域
给我们两张鸟的图片,它们都有鸟喙,但是它们的鸟喙在图片上的不同区域上,那对于每一个感受野来说,都需要配置一个专门的鸟喙检测的神经元吗?
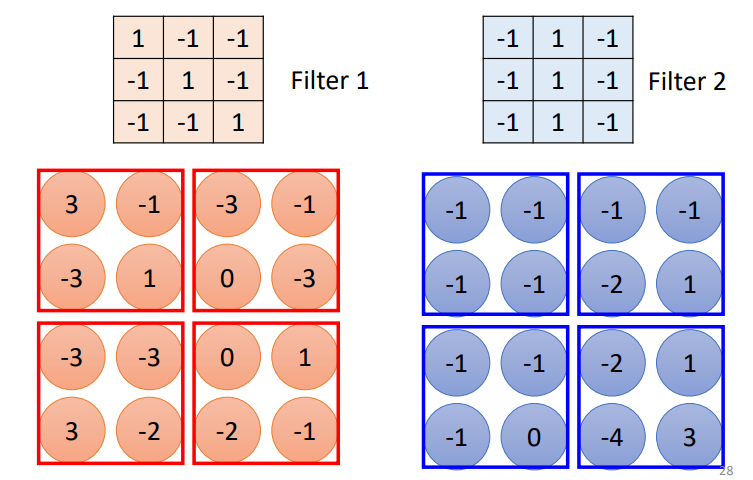
可以让所有感受野中相应的神经元来共享参数
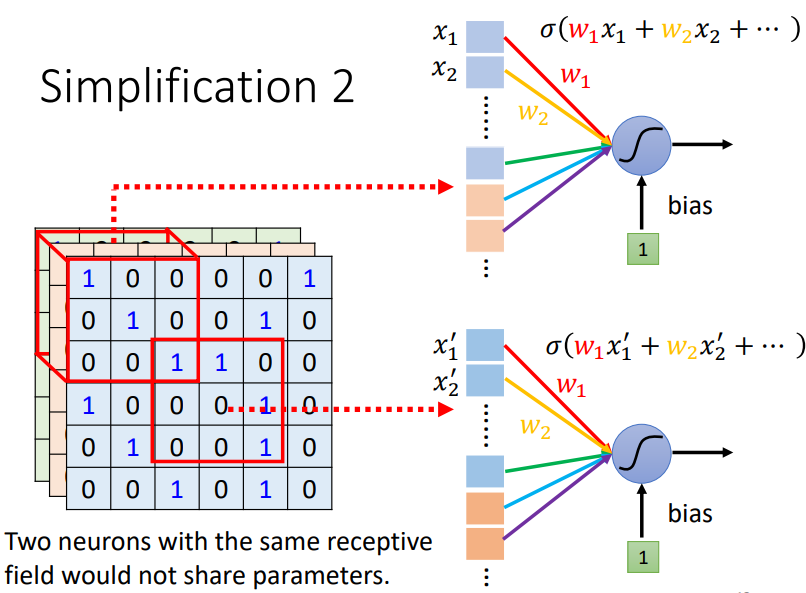
好处
- 可以很好地处理图片
- 在图片中,一些重要的pattern比整张图片要小得多
- 在不同的图片中,相同的pattern会出现在图片的不同区域
卷积层
- 彩色:3个通道
- 黑白/灰:1个通道
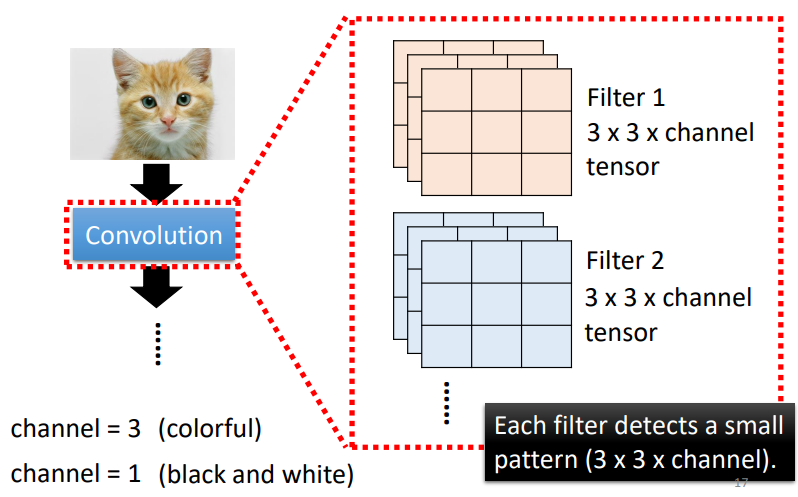
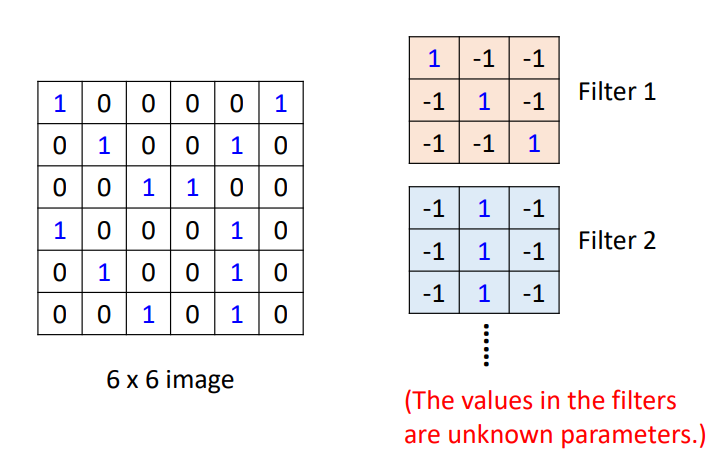
假设我们的通道为1,现在我们拥有一张6*6图片,在给定的filter中,它们的值是不确定的,需要训练得到
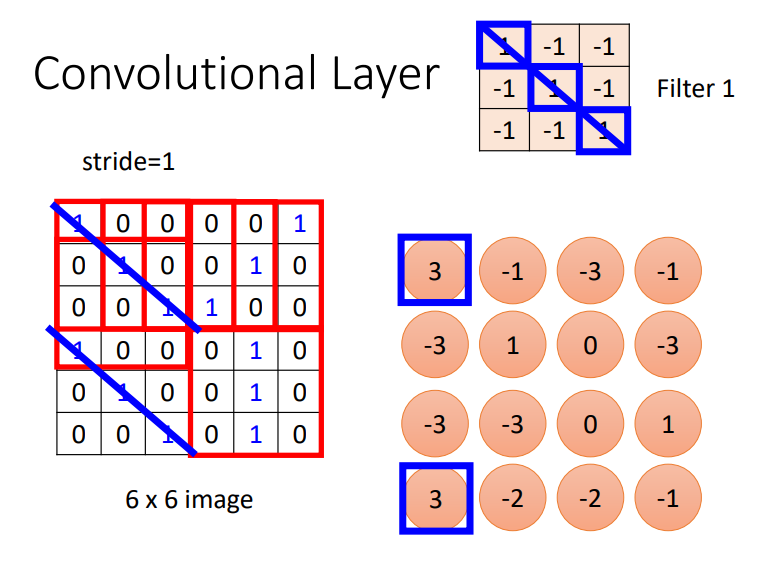
进行卷积操作后得到的数据的结构
列数: \[ (c - c_f + 1 + padding*2)\ / \ stride \]
行数: \[ (r - r_f + 1 + padding * 2)\ / \ stride \]
其中,
\(c\): 当前输入矩阵的列数
\(c_f\): filter的列数
\(r\): 当前输入矩阵的行数
\(r_f\): filter的行数
padding: 指在输入矩阵外圈填充的圈数
stride: 指filter在移动时跨越的步数
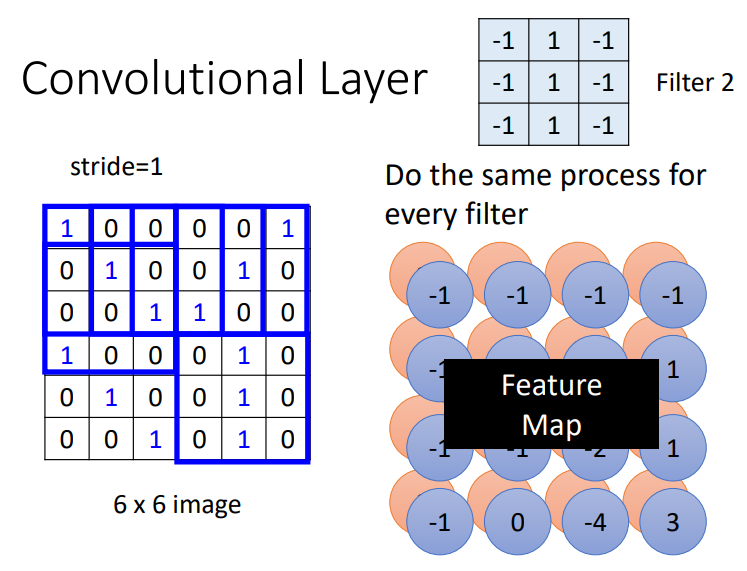
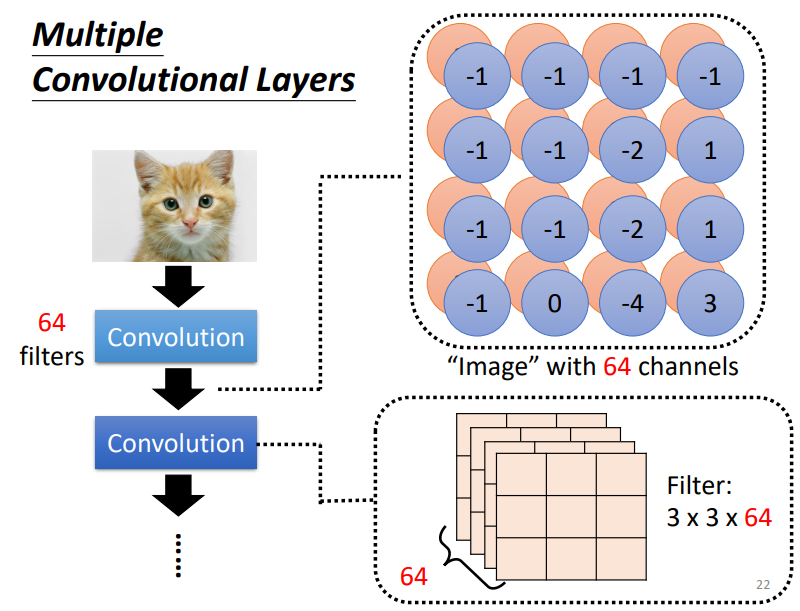
当所有的filter都对输入进行处理后,我们便获得了Feature Map,每一个filter都是对图片的不同解读,即拓展了查看图片的角度
- 我们可以将Feature Map投入到下一个卷积层中
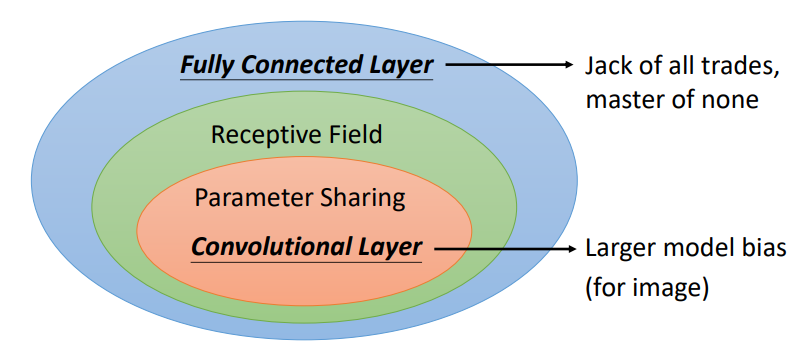
感受野和滤波器的比较
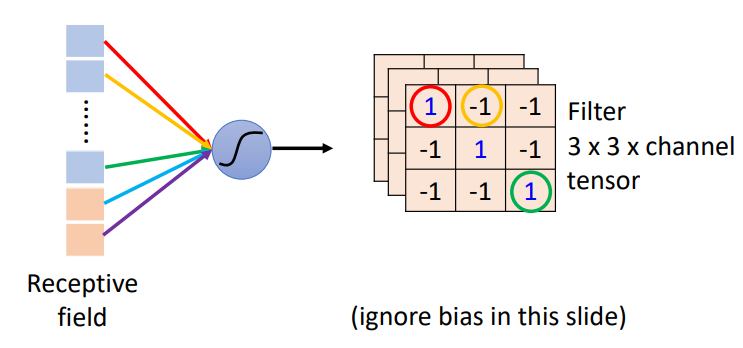
- 拥有不同感受野的神经元会共享相同的参数
- 每个滤波器会在整张输入图片上进行卷积操作

Pooling
对像素进行子采样不会更改对象
- 子采样是一种选取原始数据的子集的方法,用来减小数据的大小
- 子采样会改变数据集的拓扑,当某些部分没有被选取时,会留下拓扑上的洞
Max Pooling
选取Filter中最大的值作为感受野的取值
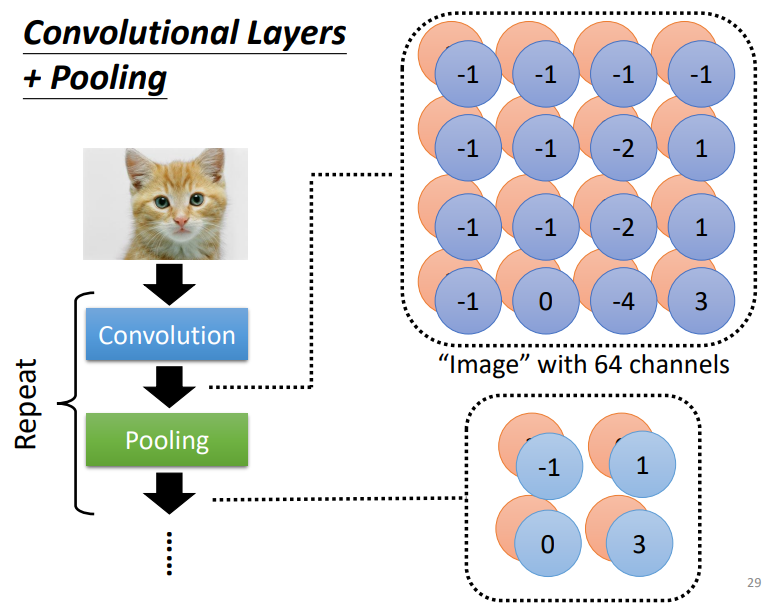
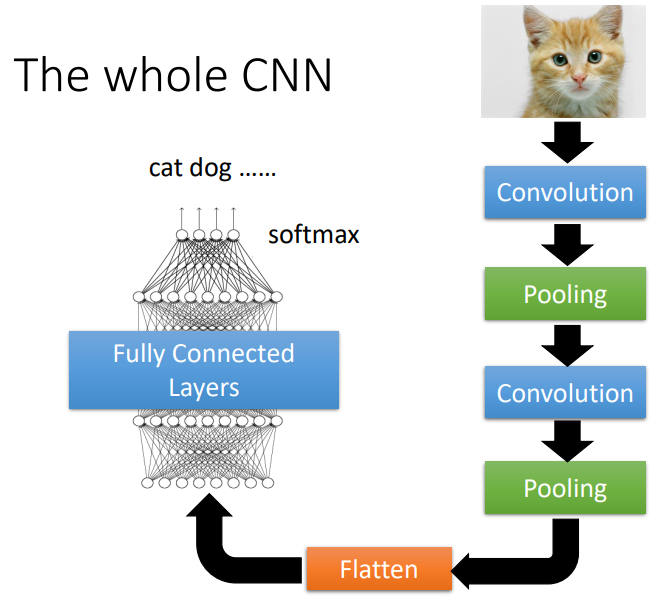
小结
- CNN能够捕捉局部信息,当使用CNN时,我们应该考虑我们的数据集和目标,是否适用CNN
- 例如Alpha Go中,在围棋中,我们需要去考虑局部的信息,而且在这种具体的情况中,pooling并不适用,子采样会损失围棋分布的信息
- CNN在图像的放缩和旋转后,不能够正常的识别,需要我们进行数据增强(data augmentation)
Recurent Neural Network(RNN)
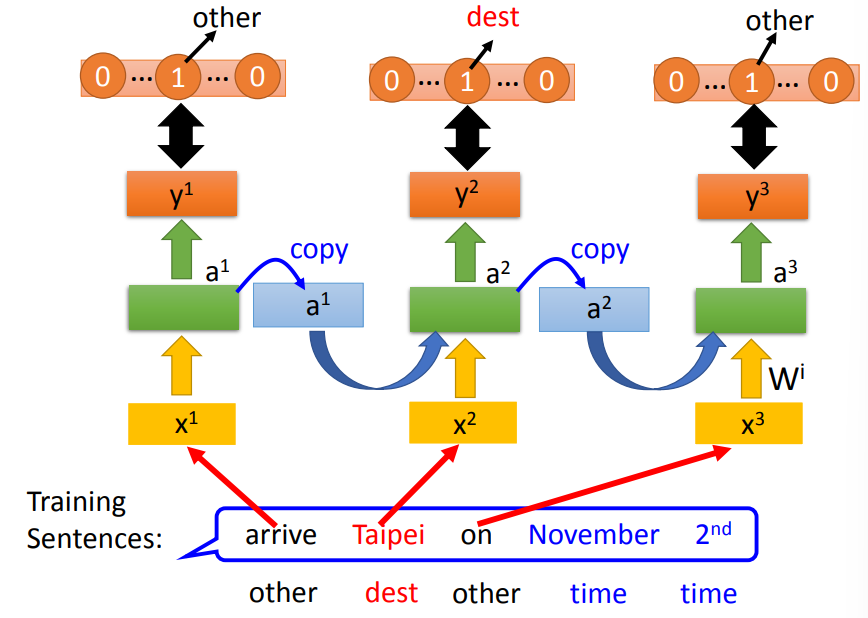
Slot Filling
- 输入一段语句,给出填空的答案
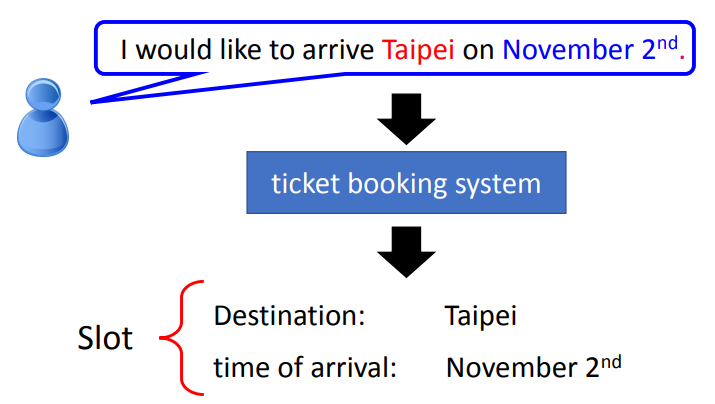
- 可不可以使用前向网络(Feedforward network)来实现
- 输入单词(使用单词编码),每一个单词用一个向量来表示
- 输出单词属于某一个空的概率
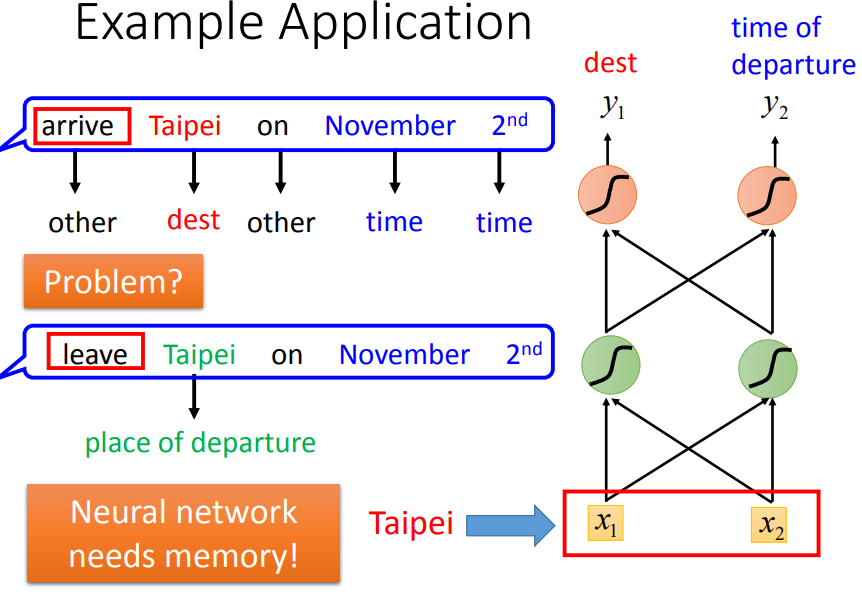
- 问题:网络无法结合上下单词,理解词汇的意义,如到达和离开的区别,只能捕捉到目的地单词
- 我们需要网络具有记忆的功能,能够记住前后的单词
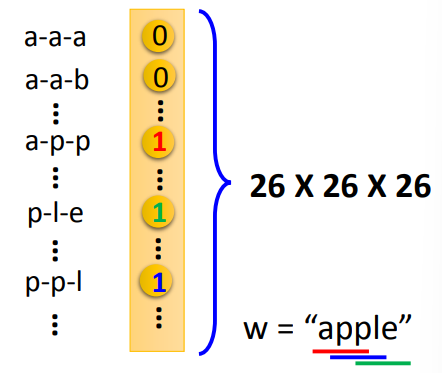
单词编码
1-of-N encoding
- 向量长度为整个词库的词语数量
- 一个维度标记词库中的一个单词
- 对于某一个单词,它所在维度为1,其他维度为0
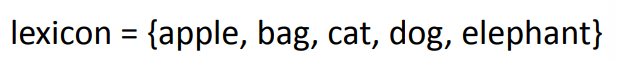

改进
Others
- 将其他不存在词库中的单词设置为“other”
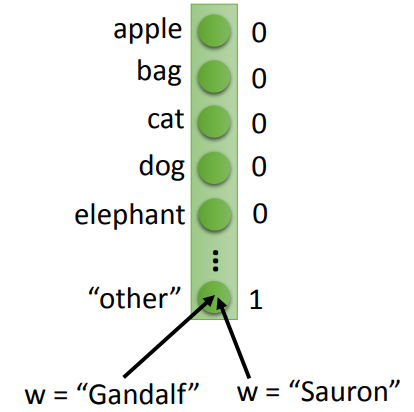
Word hashing
- 维度用来标记字母组合
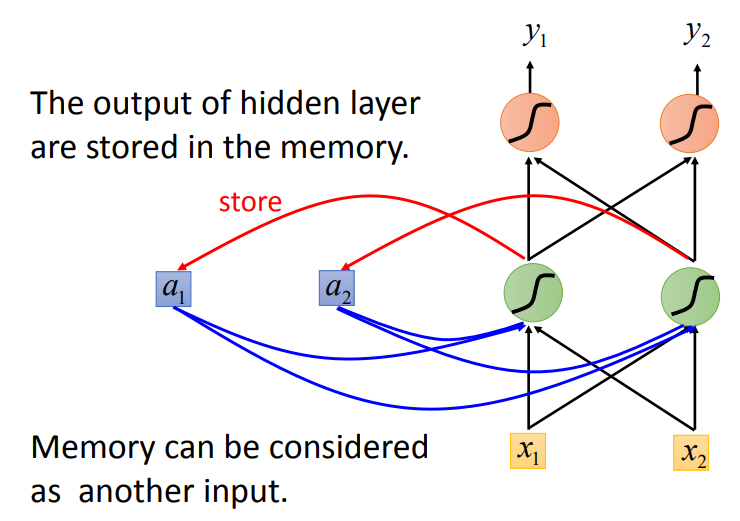
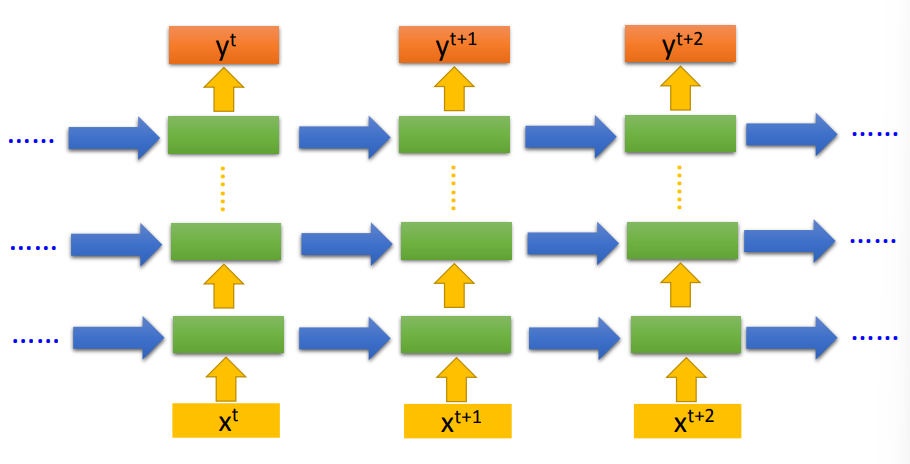
RNN
存储前一个输入的信息
- 将隐藏层的信息存储起来,将该信息作为输入,让网络可以学习
例子
假设所有的权重为1,没有bias,激活函数都是线性的
输入序列: \[ \begin{equation} \begin{bmatrix} 1 \\ 1 \end{bmatrix} \begin{bmatrix} 1 \\ 1 \end{bmatrix} \begin{bmatrix} 2 \\ 2 \end{bmatrix} \end{equation} \]
初始的存储值为0
第一次输入: \[
\begin{bmatrix}
1 \\
1
\end{bmatrix}
\] 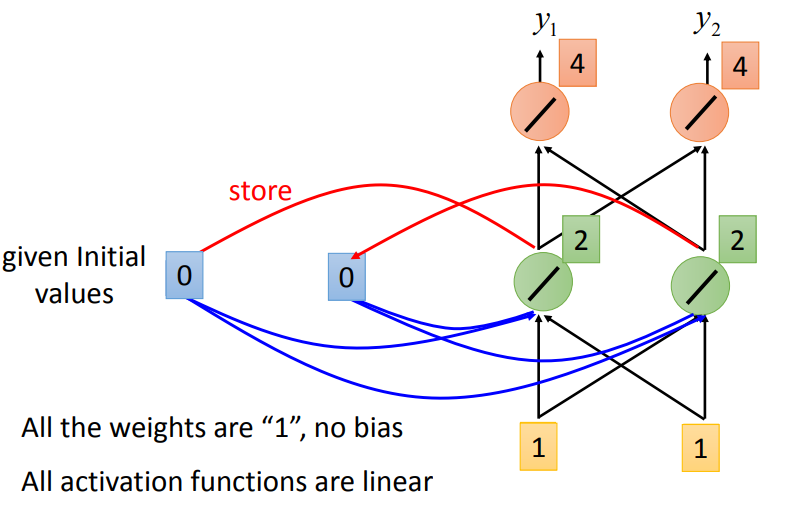
两个存储值都会变为2
输出为 \[ \begin{bmatrix} 4 \\ 4 \end{bmatrix} \]
第二次输入: \[
\begin{bmatrix}
1 \\
1
\end{bmatrix}
\] 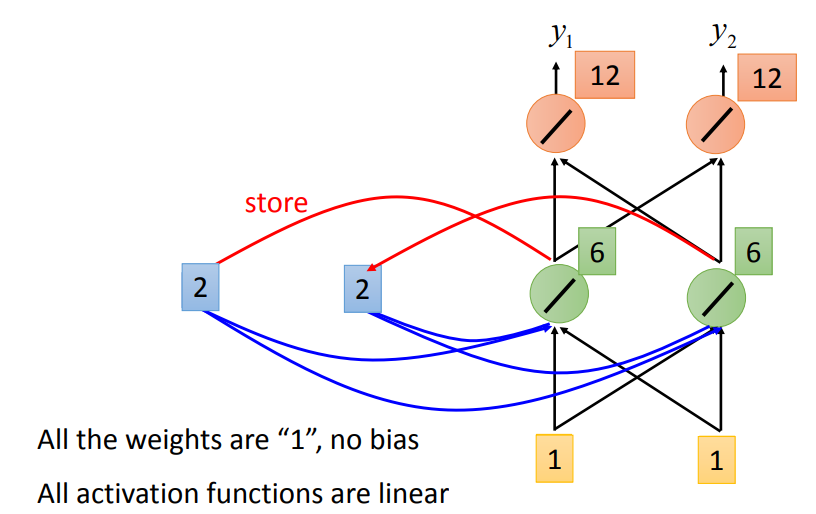
- 两个存储值会变为6
- 输出为
\[ \begin{bmatrix} 12 \\ 12 \end{bmatrix} \]
小结
- 改变输入序列的顺序,会改变输出
- 反复使用这样的结构
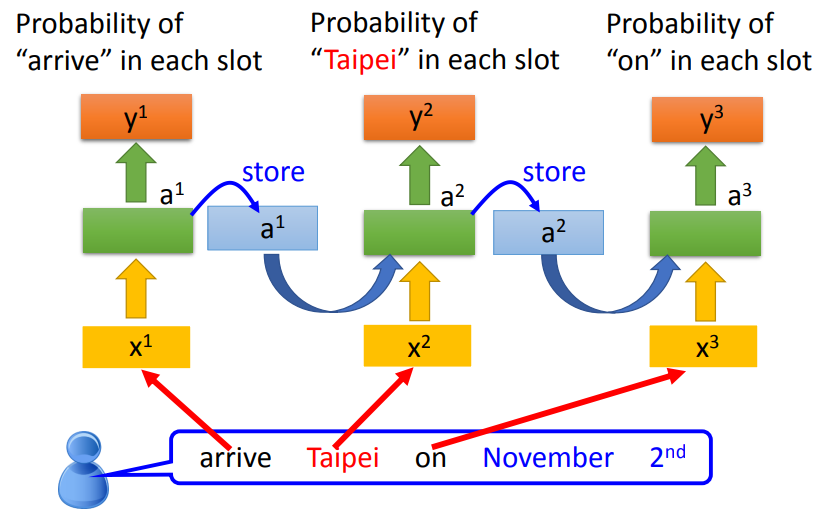
如上图所示,当前输入,可以获得前一个输入的信息,可以简单区分出一些不同
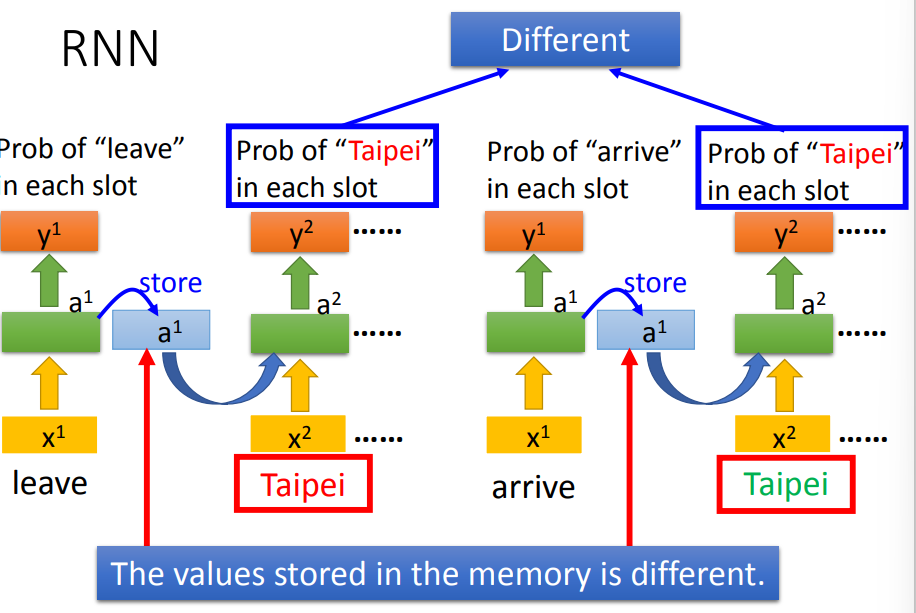
- 可以将网络做深
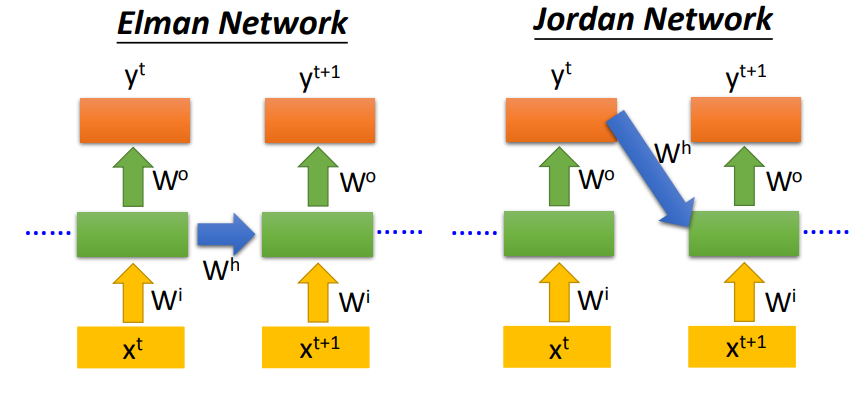
类别
- Elman Network:传递前一个输入的隐藏层信息
- Jordan Network:传递前一个输出的信息
双向RNN
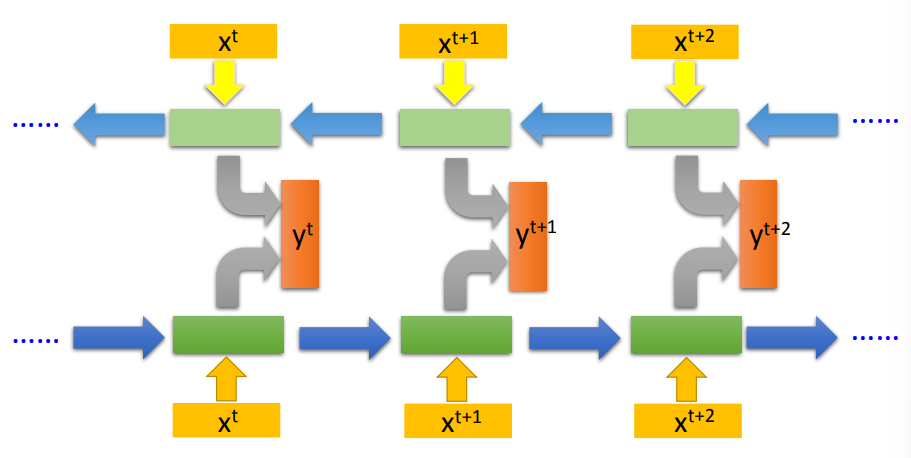
将前向输入和逆向输入相同位置上的隐藏信息拼合到一个,存储当前单词前后的信息
LSTM
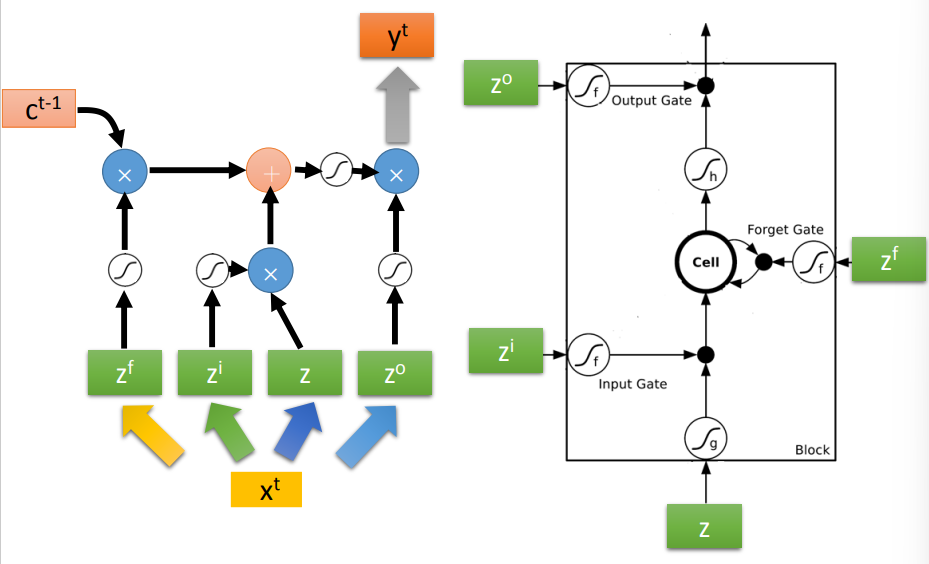
结构
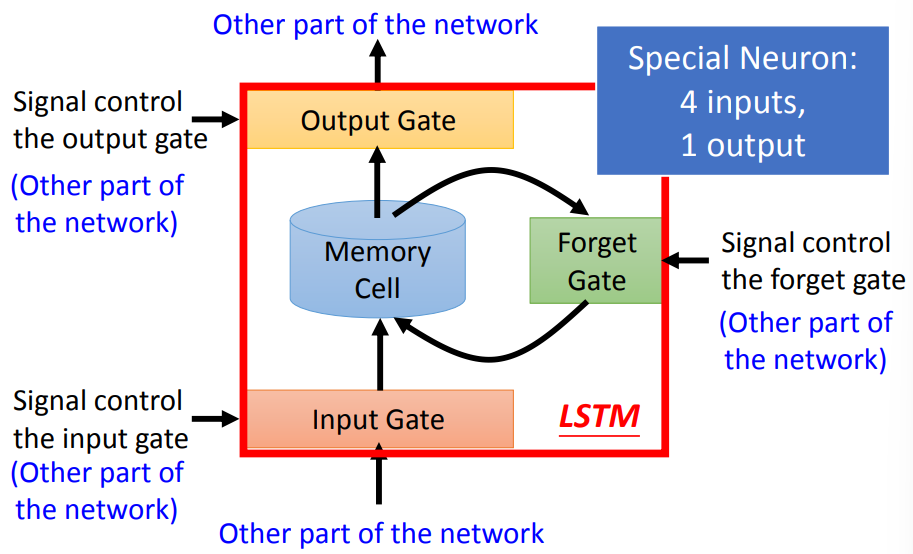
由4个部分组成
- Input Gate:由信号控制是否接收输入
- Memory Cell:存储记忆的信息
- Forget Gate:由信号控制是否清除现在存储的信息
- Output Gate:由信号控制是否输出
一共有4个输入,1个输出
- 输入:3个signal,1个正常输入
计算过程
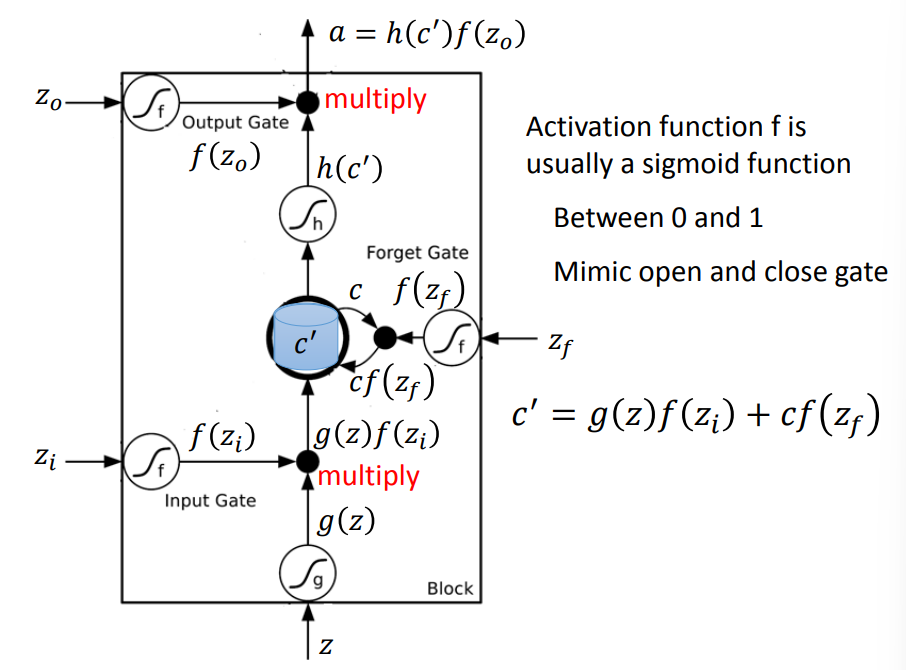
- 激活函数f输出为0到1,可以用来控制是否接收信息
- 输入\(z\)和\(z_i\),经过激活函数得到\(g(z)\)和\(f(z_i)\),将两者相乘,即为\(g(z)f(z_i)\)
- 这一步用来控制输入
- 输入\(z_f\),经过激活函数得到\(f(z_f)\),与Memory
Cell中存储的信息c进行相乘,即为\(cf(z_f)\)
- 这一步用来控制是否要清楚当前信息c
- 将前两步获得的数据相加获得新的存储信息\(c^\prime\)
\[ c^\prime = g(z)f(z_i) + cf(z_f) \]
输入\(c^\prime\)和\(z_o\),经过激活函数得到\(h(c^\prime)\)和\(f(z_o)\),将两者相乘,得到输出a,即 \[ a = h(c^\prime)f(z_0) \]
- 这一步用来控制输出
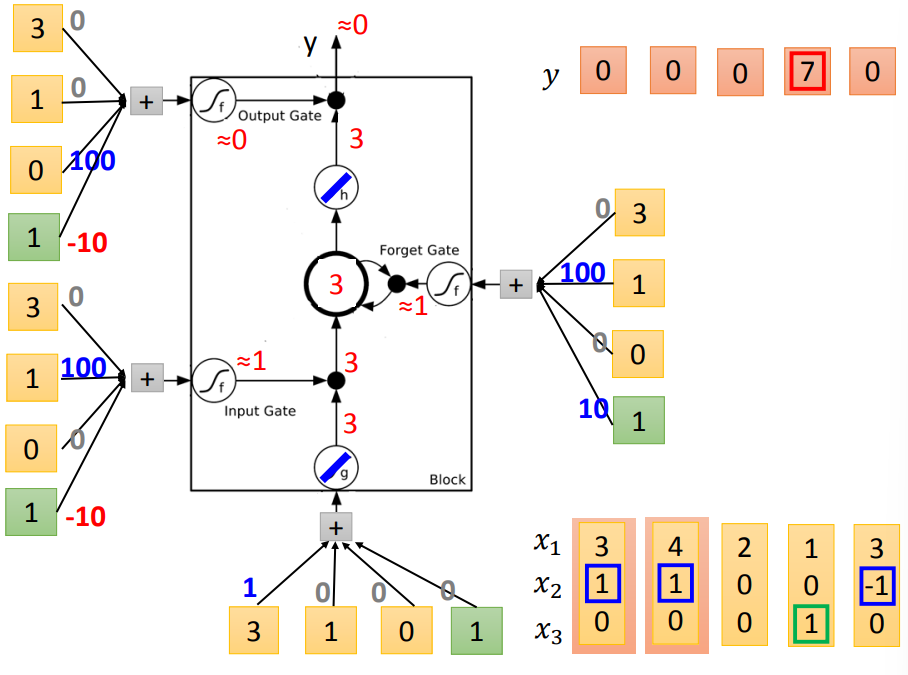
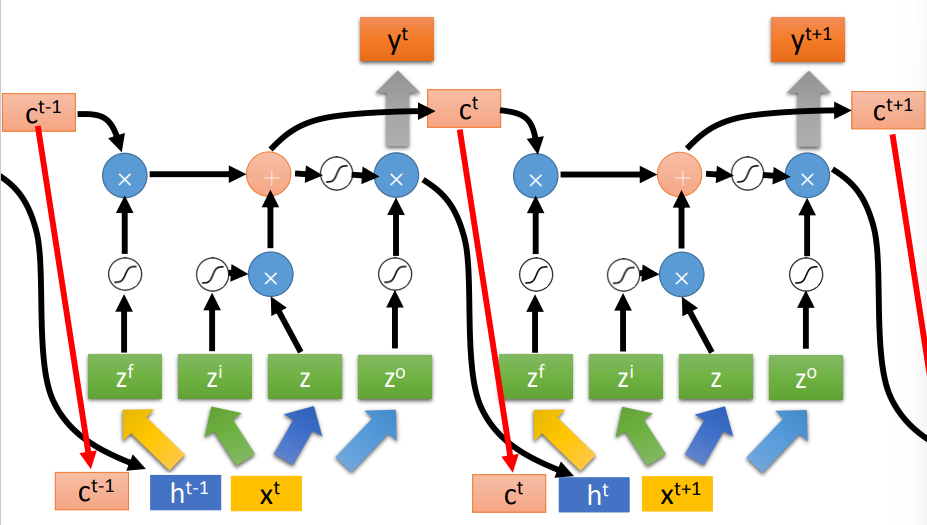
在RNN网络架构中,一般用LSTM代替神经元
缺点
参数过多
- 每一个LSTM都需要4个输入,需要4倍的参数*LSTM数目
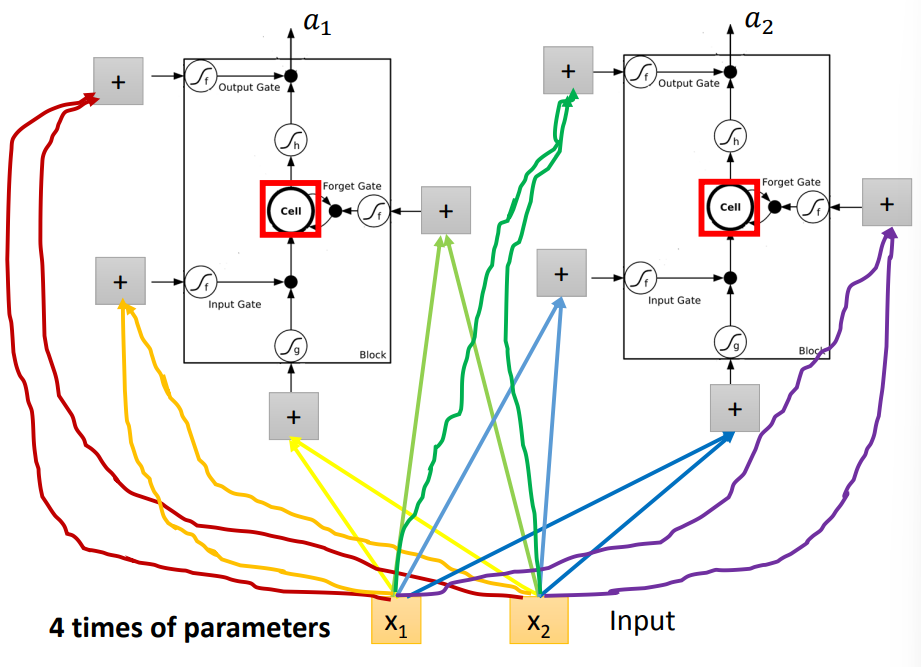
- 解决方案:利用当前输入,生成4个向量,所有的LSTM使用对应位置上的同一向量
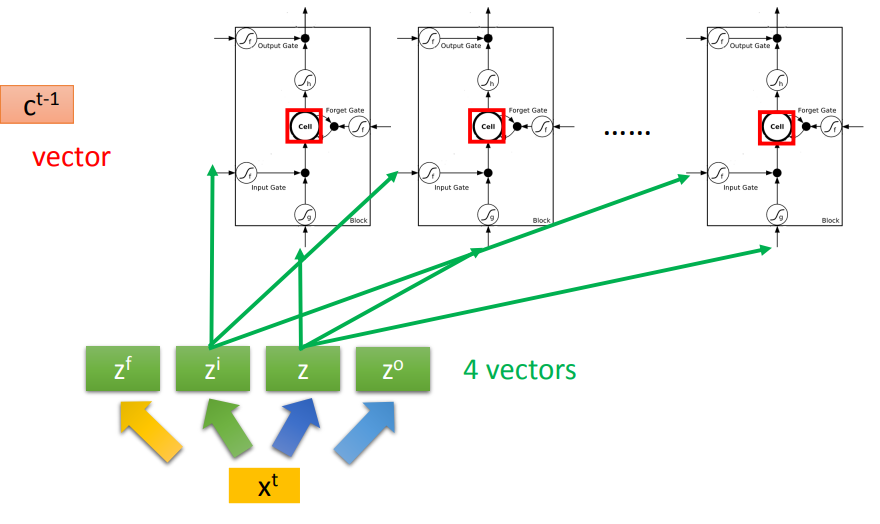
- 可以将上一个LSTM网络中的c拼合输入中
多层LSTM
学习目标
- BPTT(Backpropagation through time)
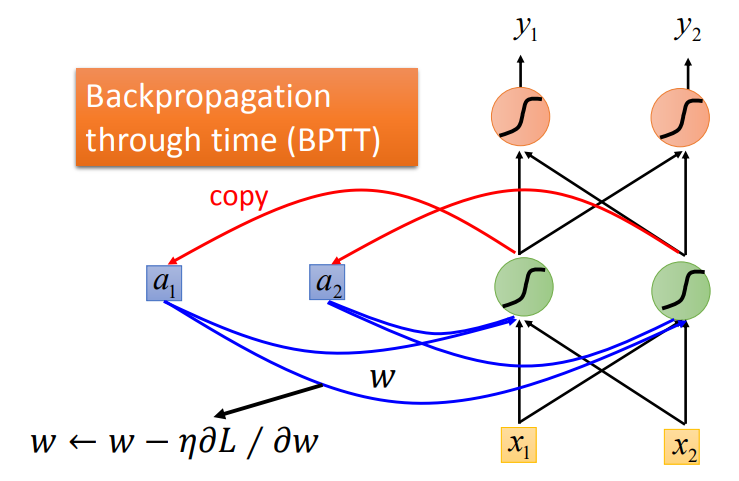
RNN训练较为困难
- RNN参数的损失曲面十分陡峭
- 可以采用clip,剪切掉超过某一范围的参数,强制在一定范围内
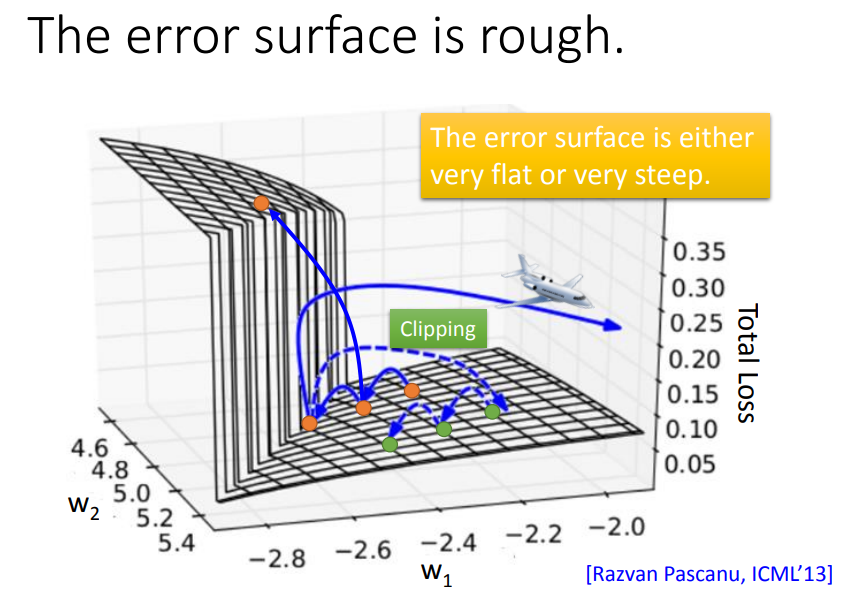
- 损失曲面会抖动严重的原因
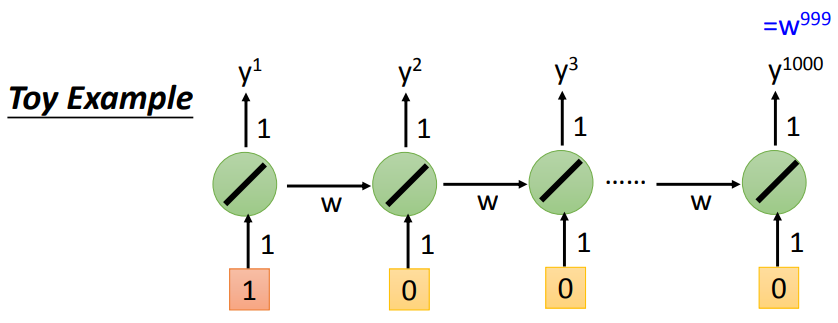
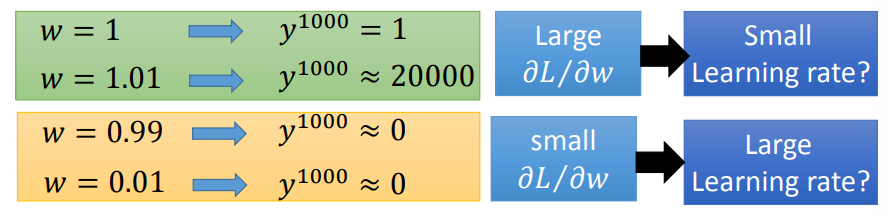
参数的细微改变,会导致后面的输出发生巨大变化(梯度爆炸),或者一直为0(梯度消失),学习率无法调节
LSTM的优势
- 可以解决梯度消失的问题(不是梯度爆炸)
- fotget gate关闭可以消除前面记录信息的影响,摆脱梯度消失
- 记录的信息和输入可以拼合
RNN的应用场景
Many to one
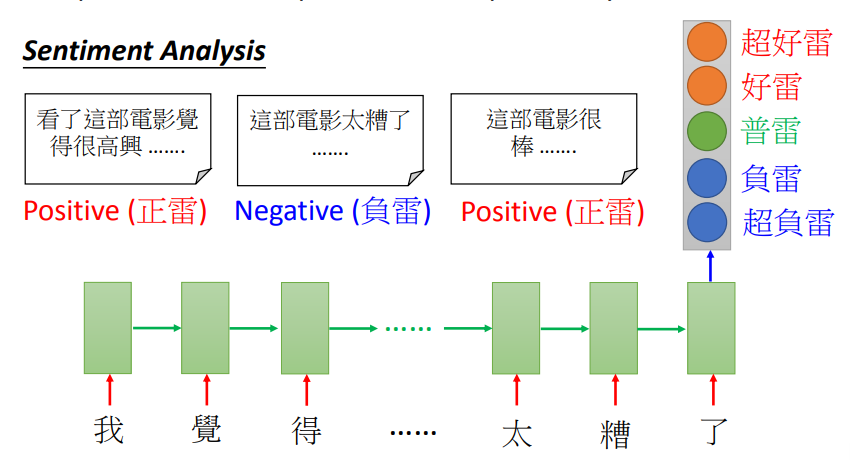
Sentiment Analysis
- 语句分析,将其分类
- 输入:向量序列
- 输出:向量标签
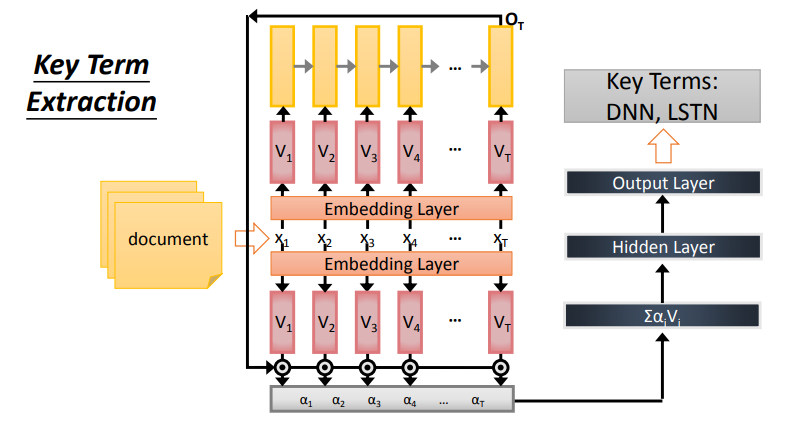
Key Term Extraction
- 关键词的提取
- 输入:向量序列
- 输出:一个向量
Many to Many(输出序列较短)
输入和输出都是序列,输出序列较短
Speech Recognition
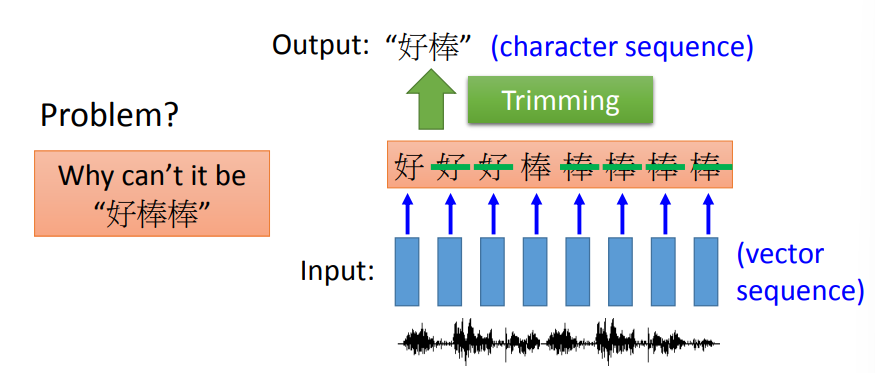
好棒棒这种叠词,可能无法识别
Connectionist Temporal Classification (CTC)
- 加入了额外的符号\(\phi\)来代表空
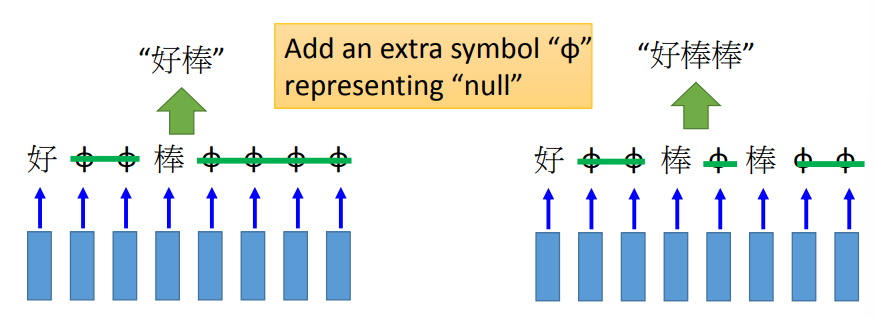
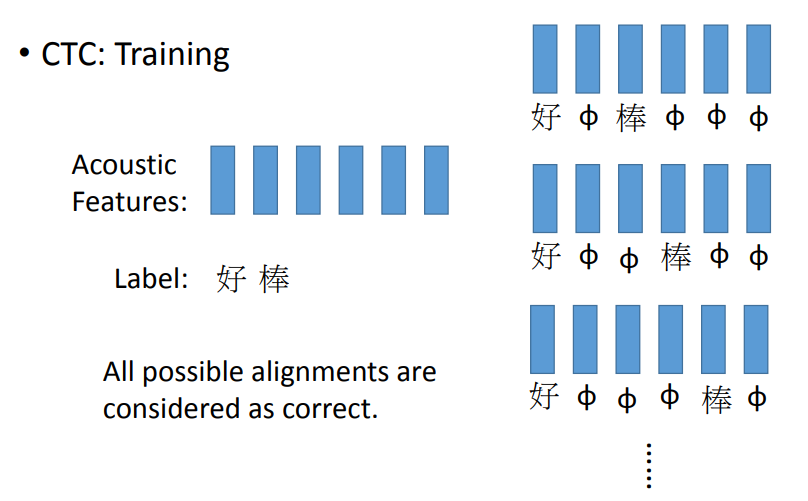
- CTC是识别每一个字母的
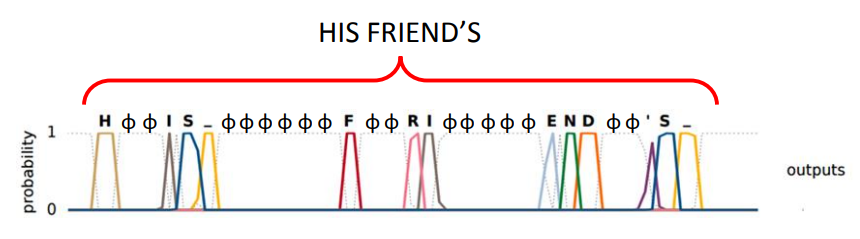
Many to Many (没有限制)
输入和输出都是序列,且长度没有限制,可以不一样 -> Sequence to sequence learning
Machine Translation
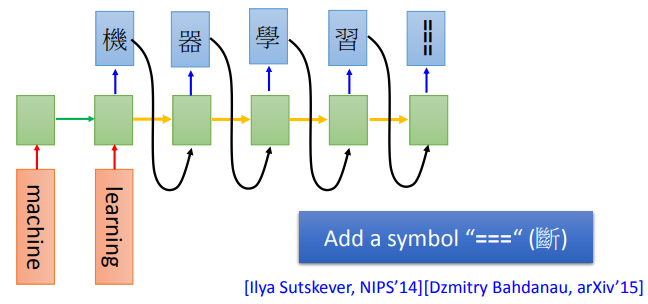
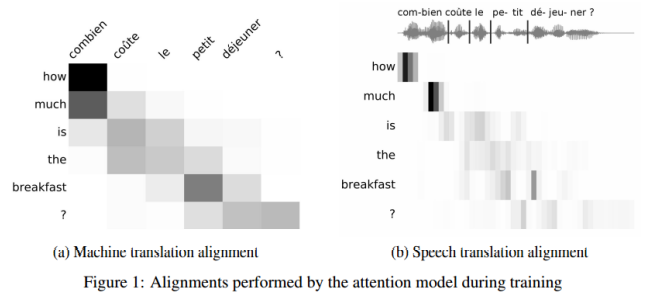
Beyond Sequence
Syntactic parsing
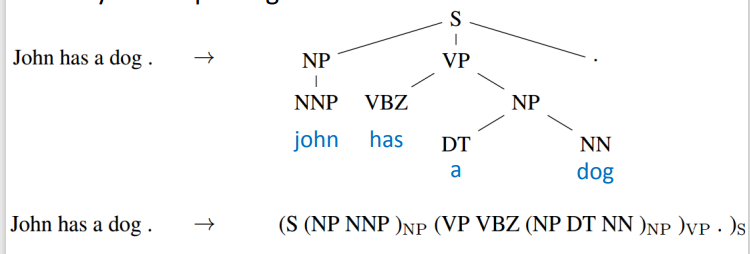
Sequence-to-sequence Auto-encoder Text
要理解一个句子的意思,单词的顺序不可以忽略

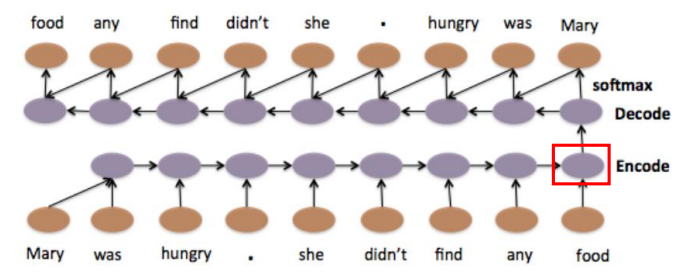
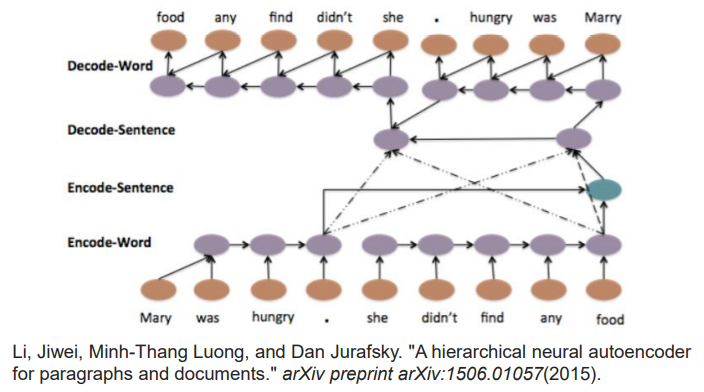
Sequence-to-sequence Auto-encoder Speech
- 不定长度的序列的降维
- 发音相近的词语转换为向量后,会聚集在一定区域
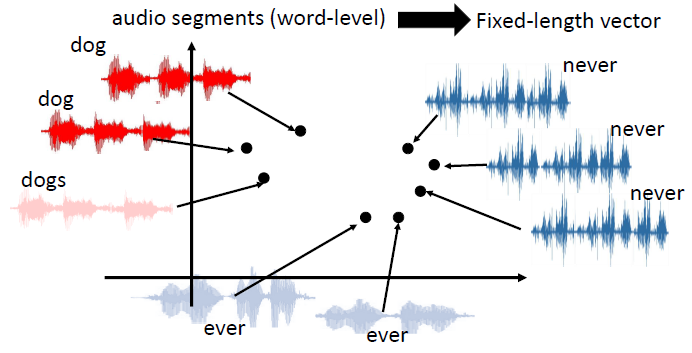
音频归档分为可变长度的音频段,然后可以对语音进行检索
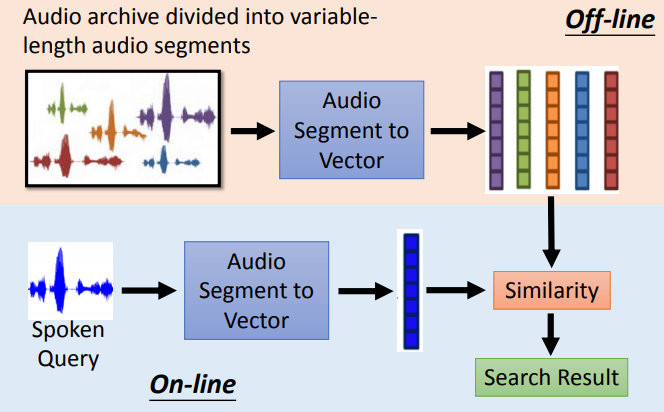
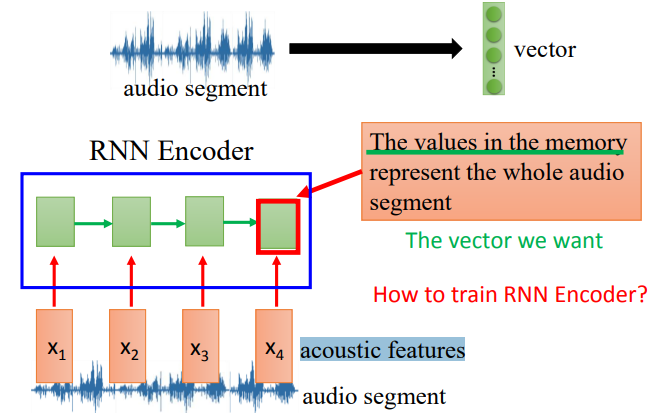
将语音片段转换为向量后,我们希望向量能够表示这个语音片段
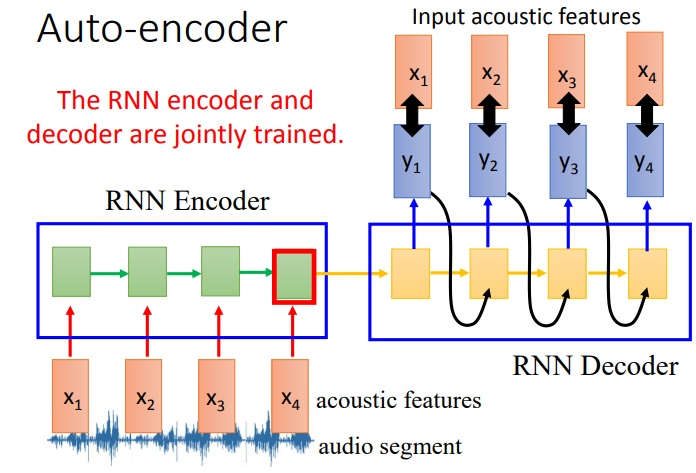
Encoder和Decoder是联合训练的
Attention-based Model
- DNN/RNN可以通过Reading Head Controller在Memory中找到自己想要的相关信息
- 就像人类的大脑一样,可以去记忆中去搜索相关的知识
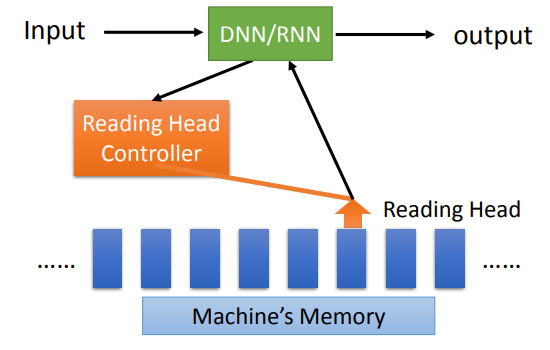
- DNN/RNN同时也可以写入Memory
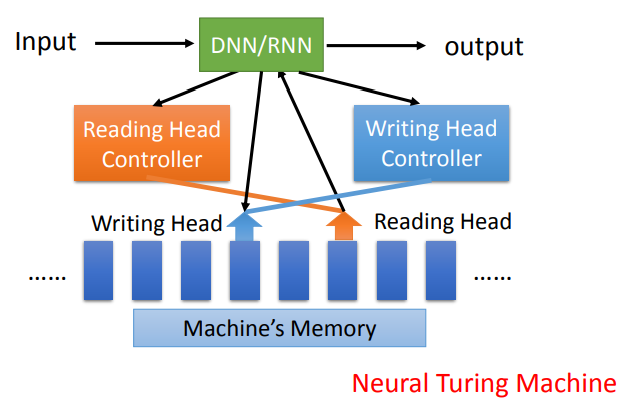
应用
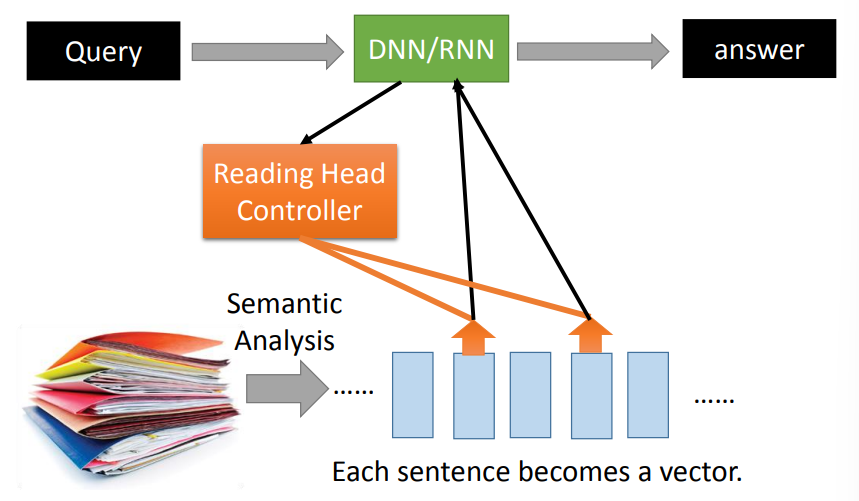
Reading Comprehension
- 对文本进行语义分析,每一个句子转换为一个向量
- DNN/RNN读取向量信息
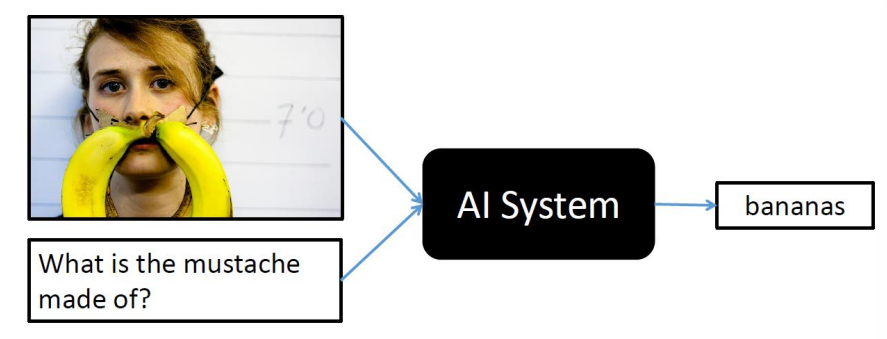
Visual Question Answering
- 输入一张图片和一个问题,输出问题的答案
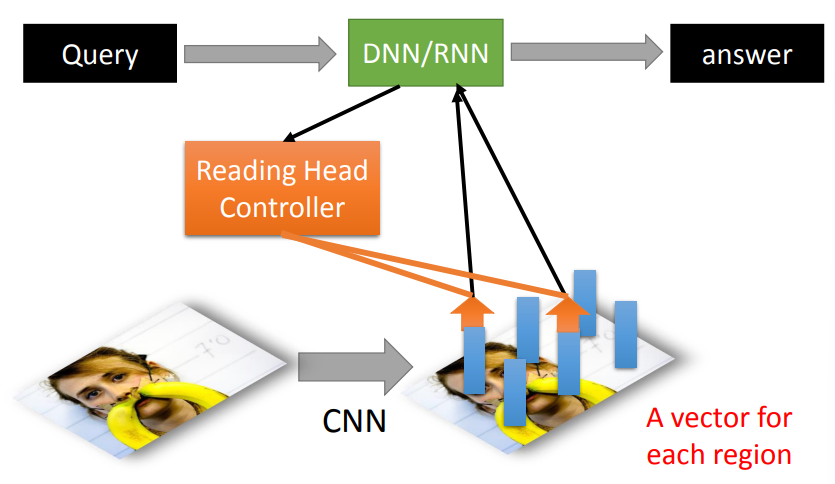
- 利用CNN将图片的每一个区域转换为一个向量
Speech Question Answering
听力考试
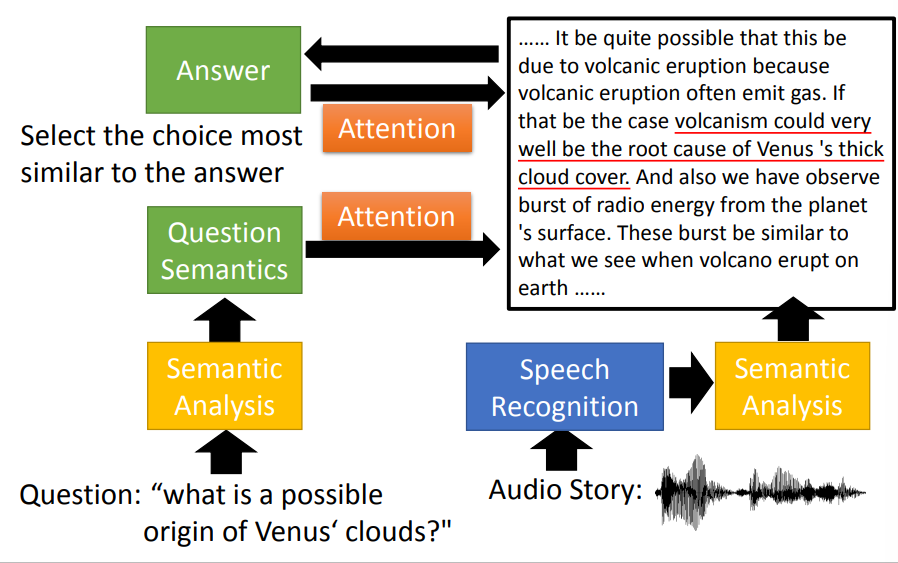
RNN和Structured Learning的比较
RNN,LSTM
- 非双向的RNN不能够考虑整个序列
- Cost和eroor总是相关的
- deep
HMM,CRF,Structured Perceptron/SVM
- 使用了Viterbi,考虑了整个序列
- 但双向的RNN也可考虑
- 可以明确考虑标签依赖关系
- Cost是error的下界

一起使用
Speech Recognition: CNN/LSTM/DNN + HMM
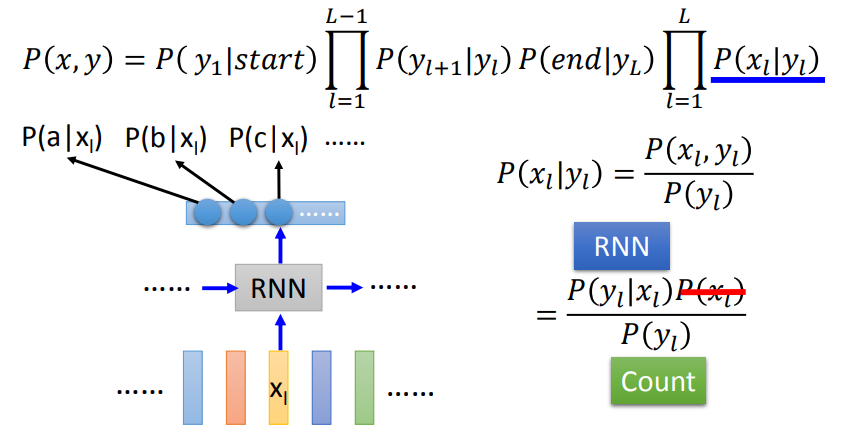
Semantic Tagging: Bi-directional LSTM + CRF/Structured SVM
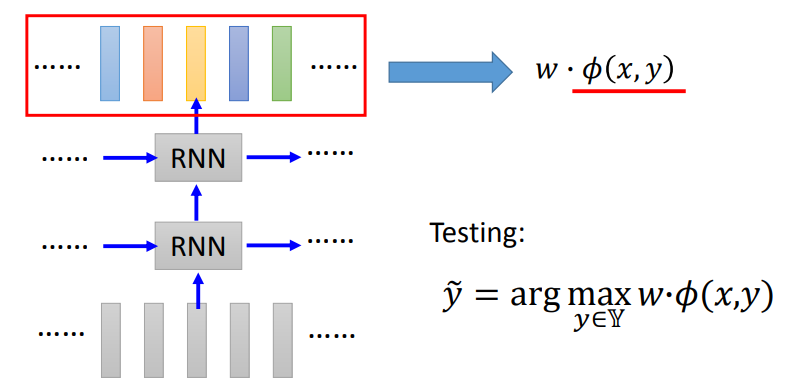
Self-Attention
输入
- 输入是一个向量,经过模型后输出一个数字或者类别
- 输入时一组向量,经过模型后输出一组数字或者类别
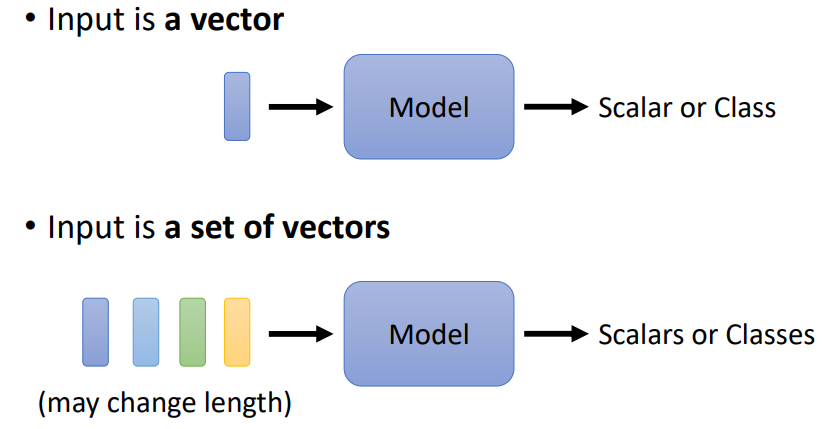
输入时是一组向量
- 语句
- 语音
- 图(如关系图)
语句
如一句话“this is a cat”,我们需要对数据集进行编码处理,以便识别各个单词
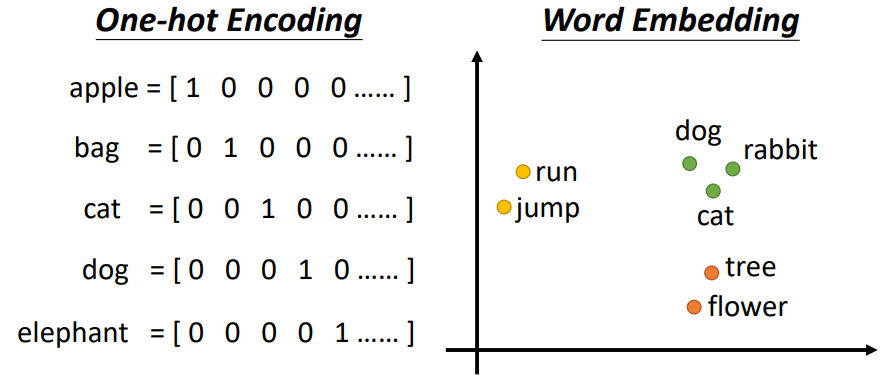
- One-hot Encoding 一键编码
- 有多少个单词,就构建一个多长的向量
- 这样做的后果是模型不知道单词之间的关系,它们是割裂的
- Word Embedding 词嵌入
- 对词语进行编码处理,相似意义的词会聚集
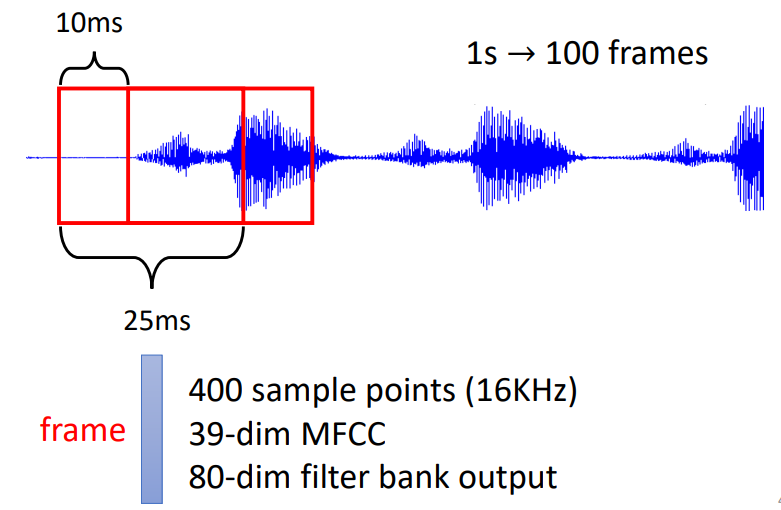
语音
进行加窗处理
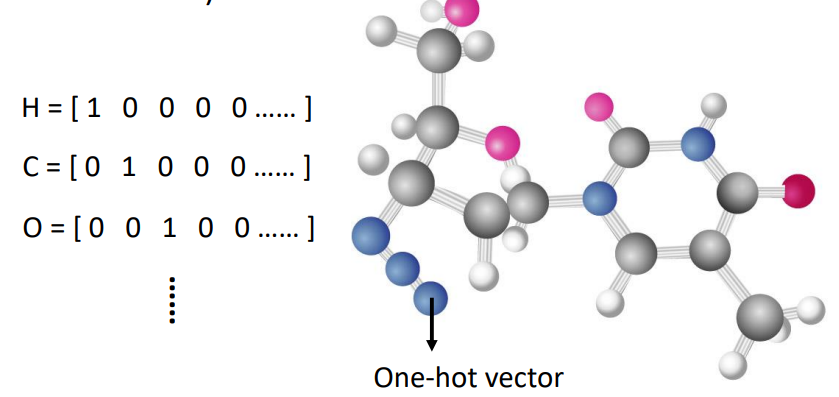
图
将每一个节点都视为一个向量
输出
- 每一个向量都有一个标签

例子
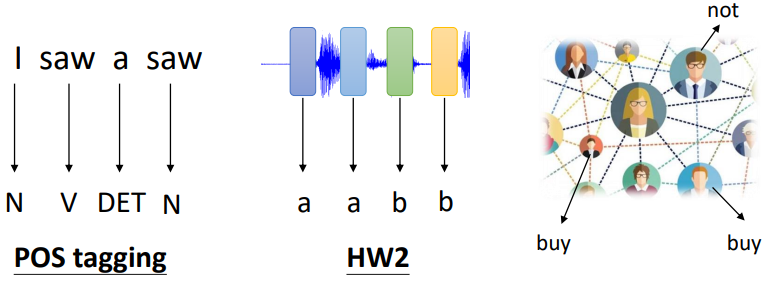
- 整个序列有一个标签

例子
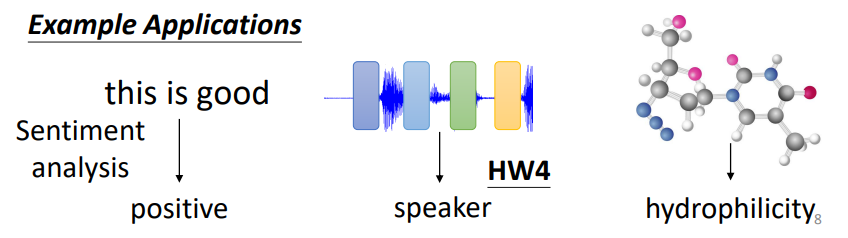
- 模型自己决定有多少个标签(seq2seq)

思考
- 对于一段文本,我们需要考虑前后文,如判断"I saw a
saw"中各个单词的词性
- 对于前后文问题,我们可以将一个窗口内的单词都输入一个全连接层中,但是这样较前面的和较后面的很难一起考虑
- 考虑整个句子,可以将整个句子丢入一个全连接层中,但是这样模型会变得很复杂
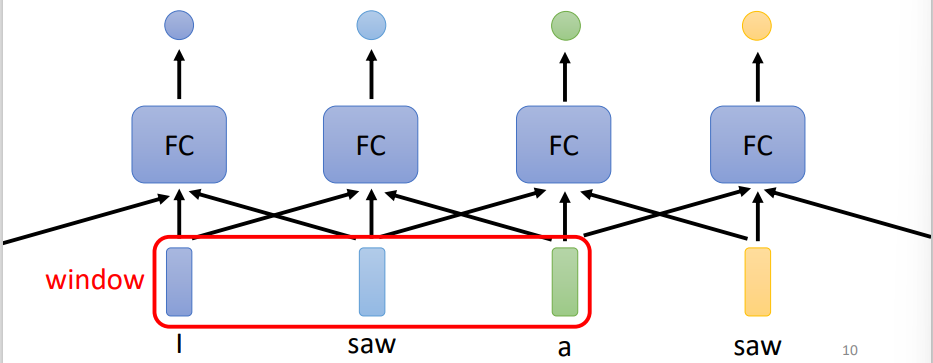
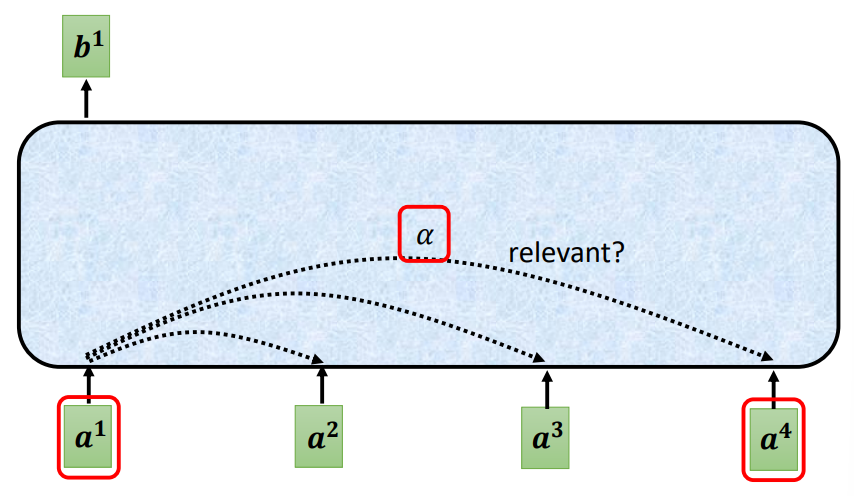
- 可以使用自注意力机制
自注意力
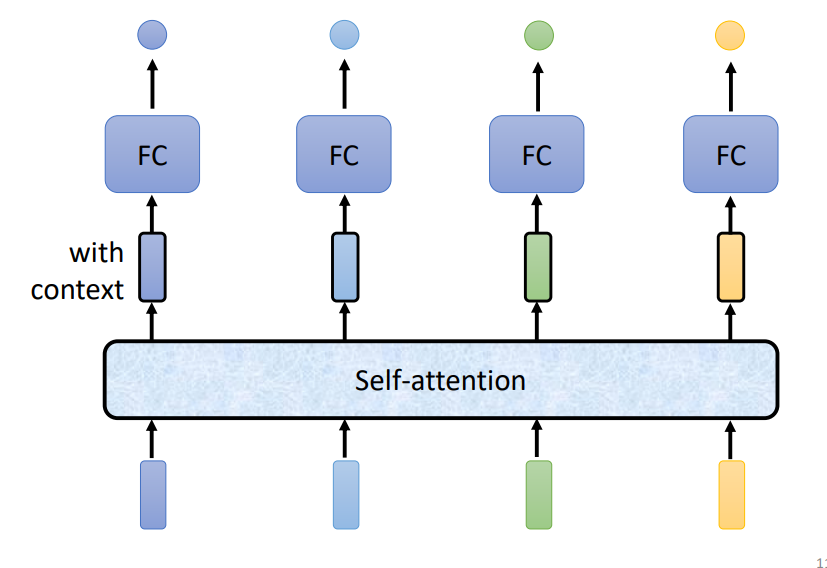
实现
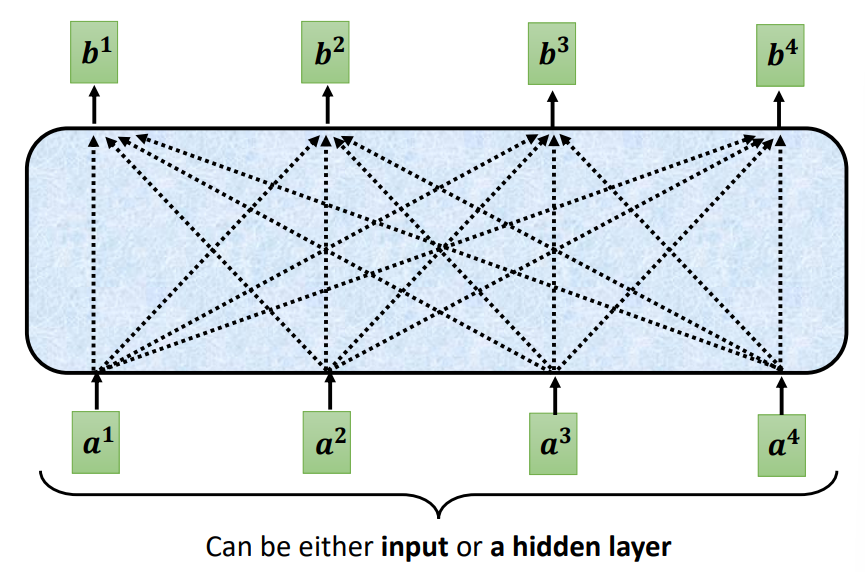
考虑当前向量和序列中其他向量的关系
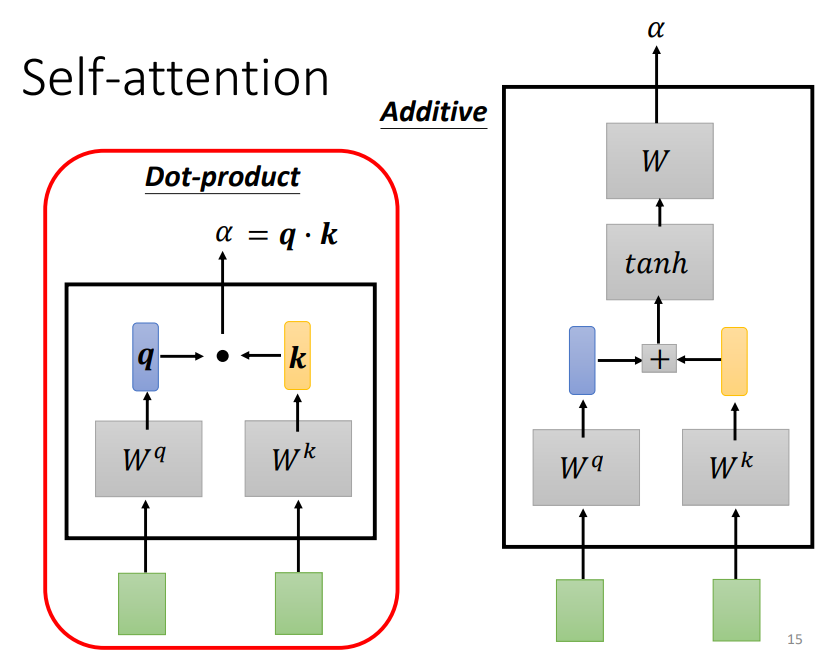
可以对两个要关联的向量进行某种运算
- Dot-product
- Additive
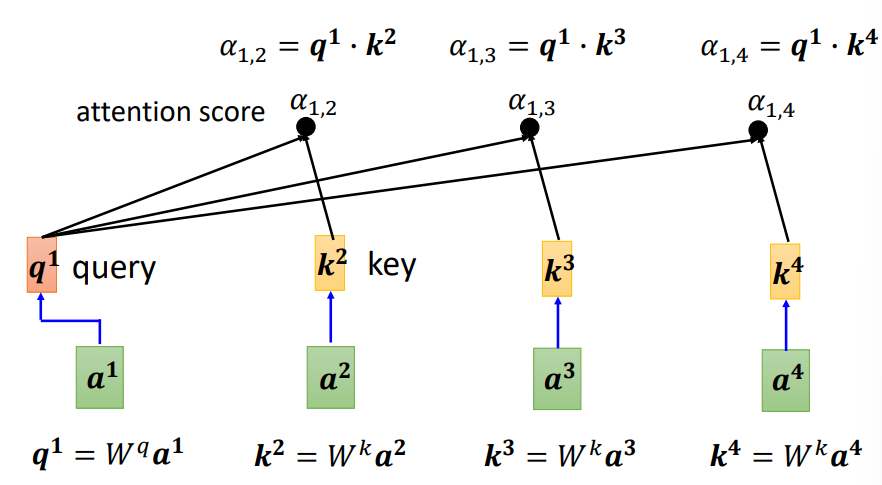
对于当前向量,计算出一个query向量,对于其他的向量,各有一个key向量,可以分别计算得出注意力分数(attention score)
可以对注意力分数(attention score)进行softmax运算
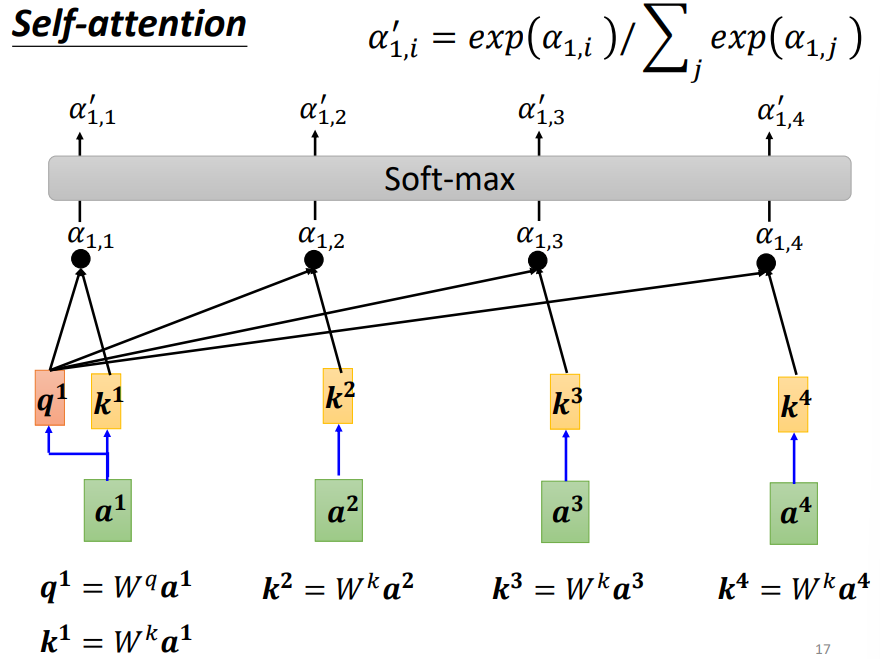
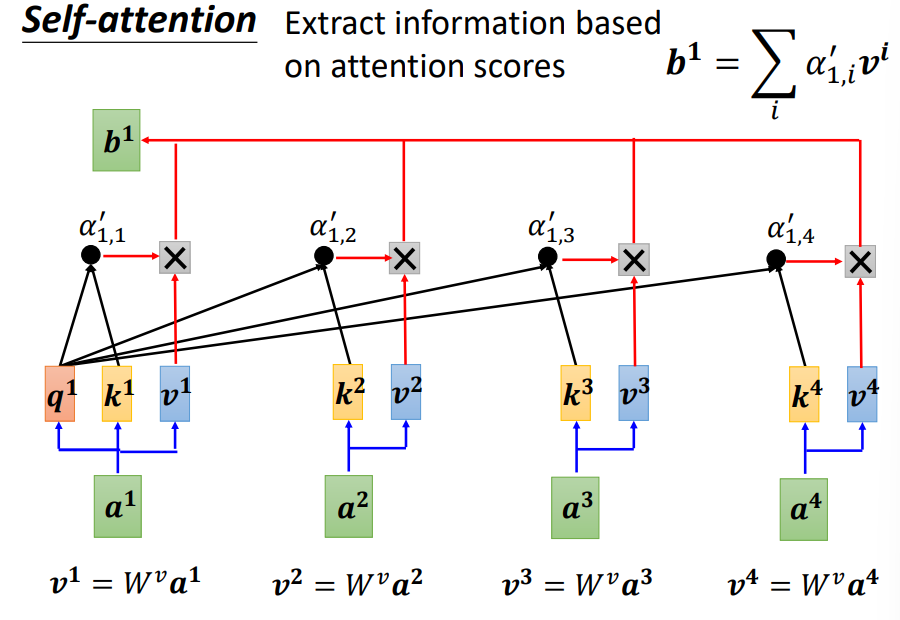
然后基于注意力分数(attention score),利用value向量,提取出信息
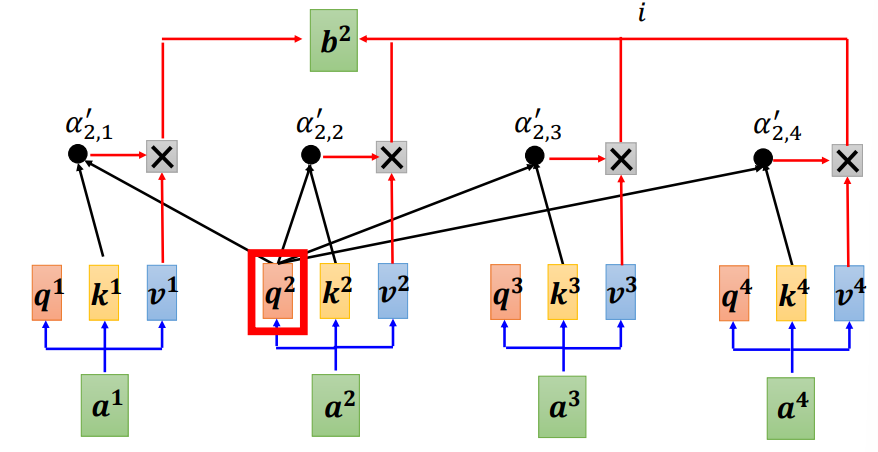
对于所有的向量,平行地进行运算

对于这样相同的运算,我们可以将这些向量拼合成矩阵,进行矩阵运算,加快运算
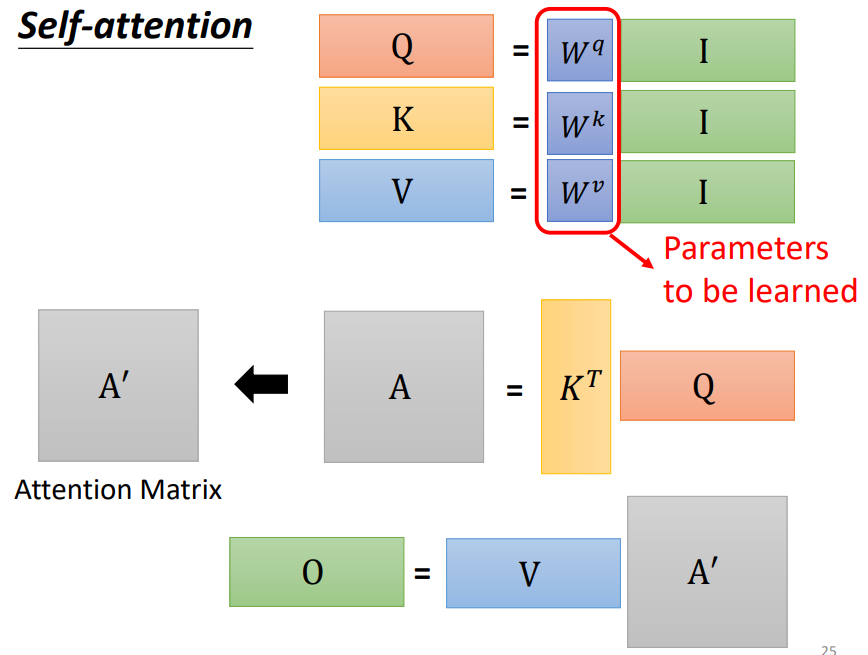
- q,k,v的获取
- query:\(Q = W^q I\)
- key:\(K = W^k I\)
- value:\(V = W^vI\)
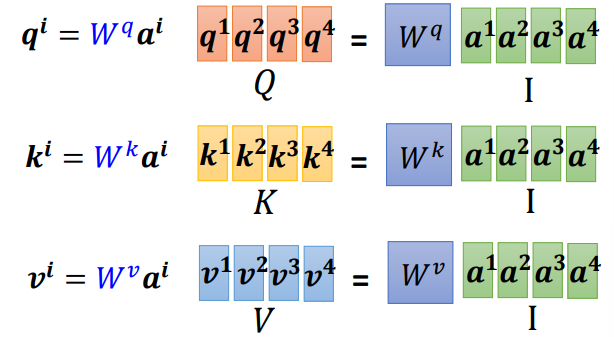
- 注意力分数的获取
\[ A = K^T Q \\ A \mathop\rightarrow^{softmax} A^` \]
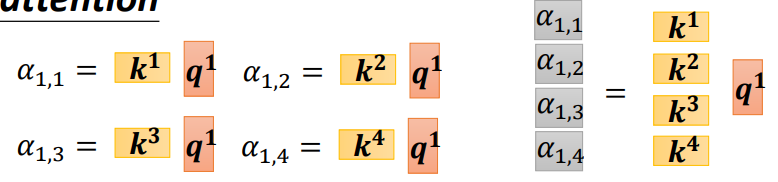

- 信息的获取
\[ O = V A^` \]
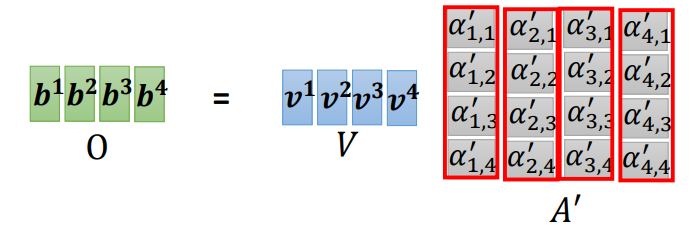
- 小结
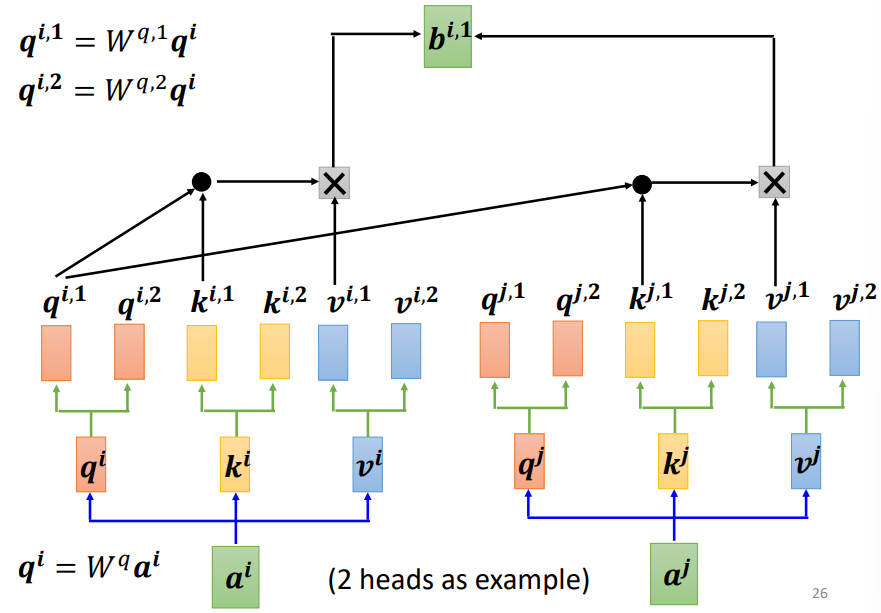
Multi-head Self-attention
- 多头注意力机制
- 可以探索不同类型之间的联系
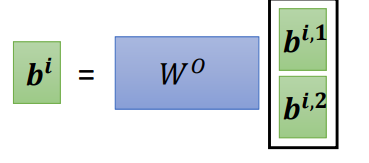
Positional Encoding
- 在注意力机制中,序列输入后,模型没有对于位置的信息,不同距离的两个向量对于模型来说是一样的
- 我们可以在向量中加入位置信息,每一个位置有一个独一无二的向量\(e^i\)
- 手工制作
- 从数据中学习
自注意力的应用
NLP 自然语言处理
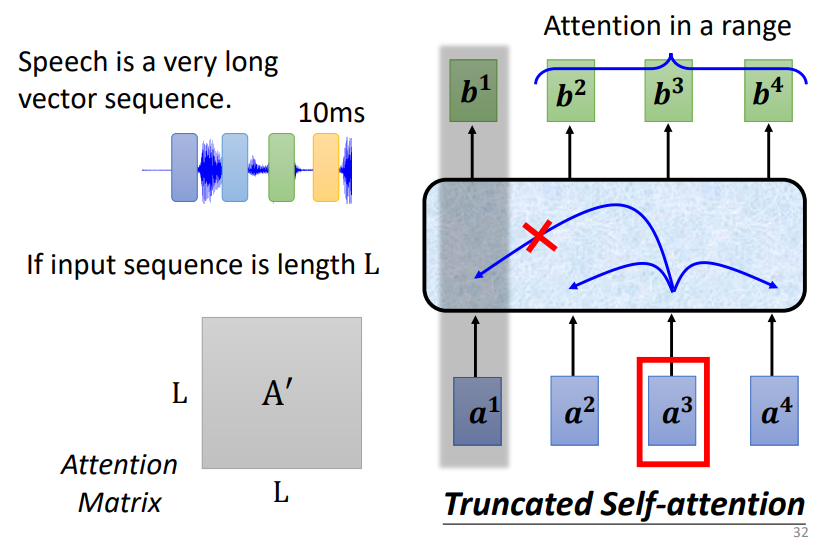
语音处理:Truncated Self-attention
- 图像
- Self-attention GAN
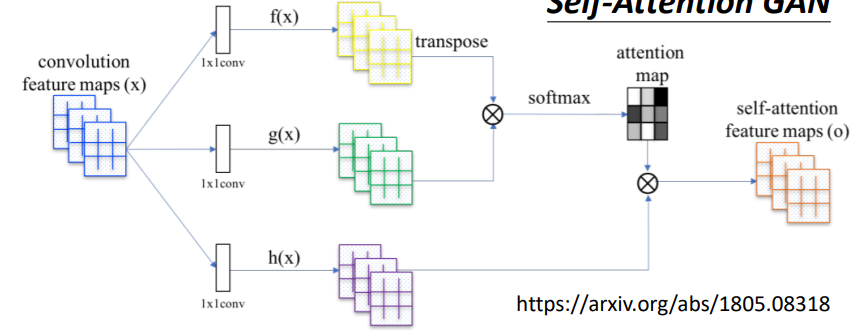
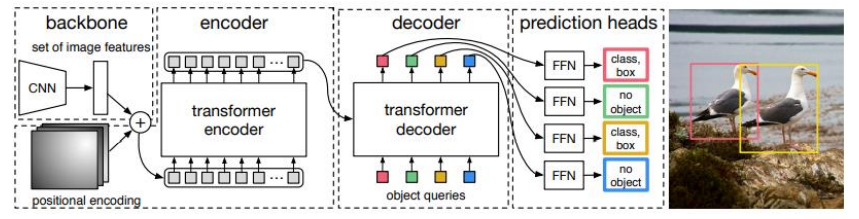
- DEtection Transformer(DETR)
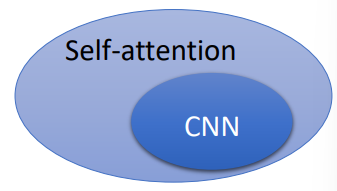
Self-attention和CNN的比较
- CNN是简化版的self-attention
- CNN是可以只关注一个感受野的self-attention
- self-attention是复杂版的CNN
- Self-attention是具有可学习感受野的CNN
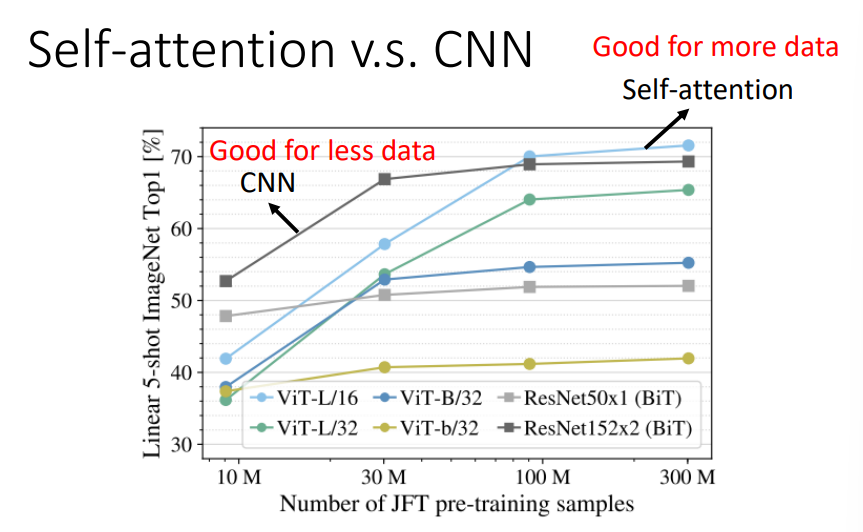
- Self-attention适合更多的数据,而CNN适合比较少的数据
Self-attention和RNN的比较
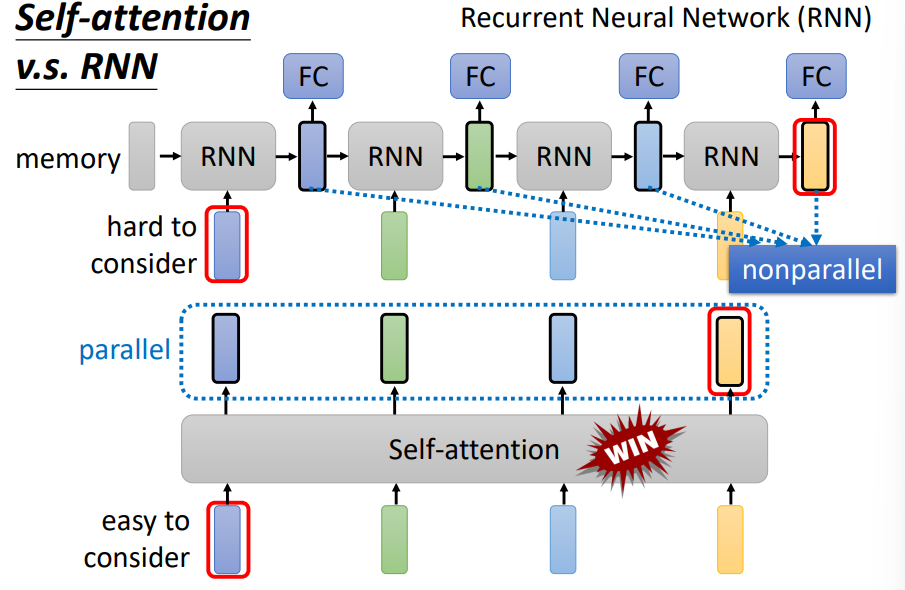
RNN不可以平行处理,而自注意力可以
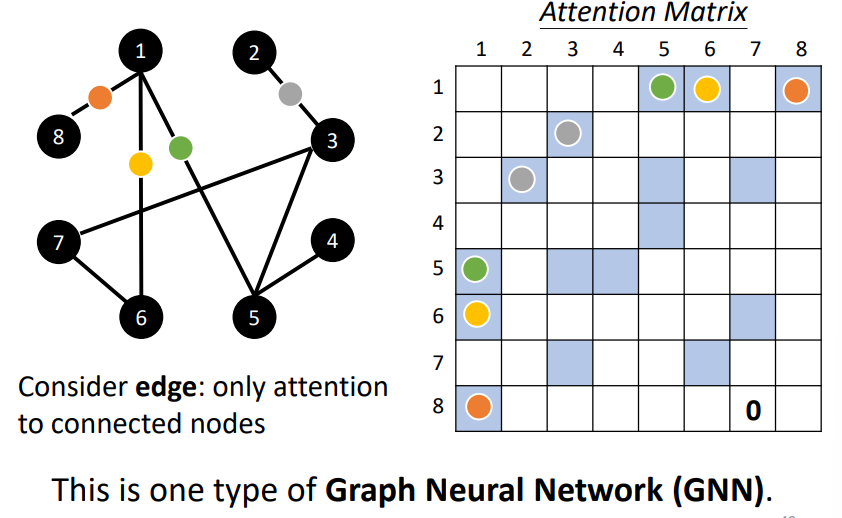
Self-attention for Graph
Transformer
Seq2seq
- 对于序列到序列的模型,我们输入一段序列,模型会输出一段序列,且输出序列的长度取决于模型
- 语音识别(Speech Recognition)
- 机器翻译(Machine Translation)
- 语音翻译(Speech Translation)
- 文本转语音合成器(Text-to-Speech(TTS) Synthesis)
- Seq2seq for Chatbot
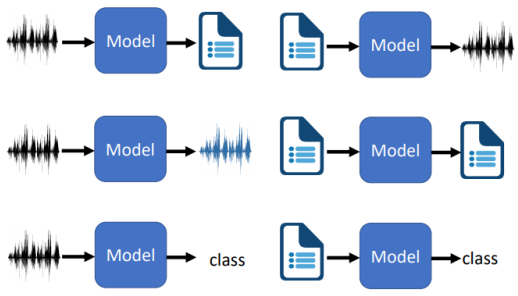
其他的一些应用
- Seq2seq for Syntactic Parsing
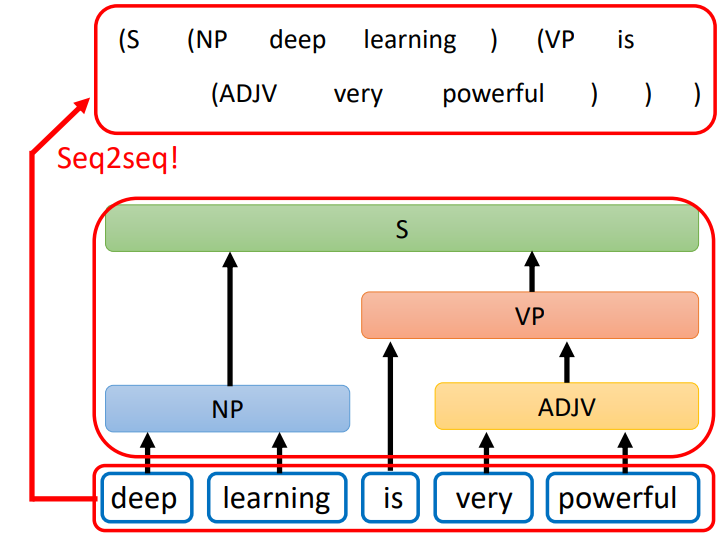
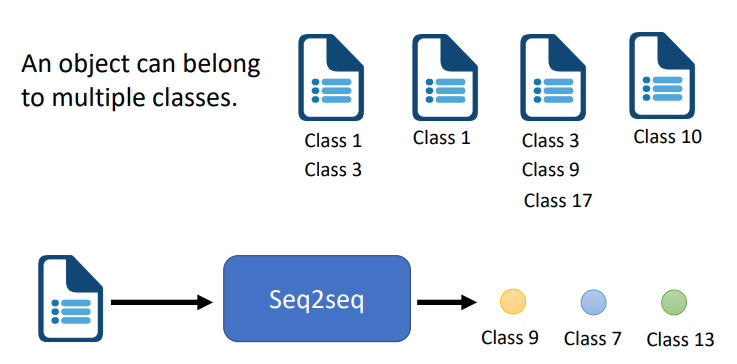
- Seq2seq for Multi-label Classification
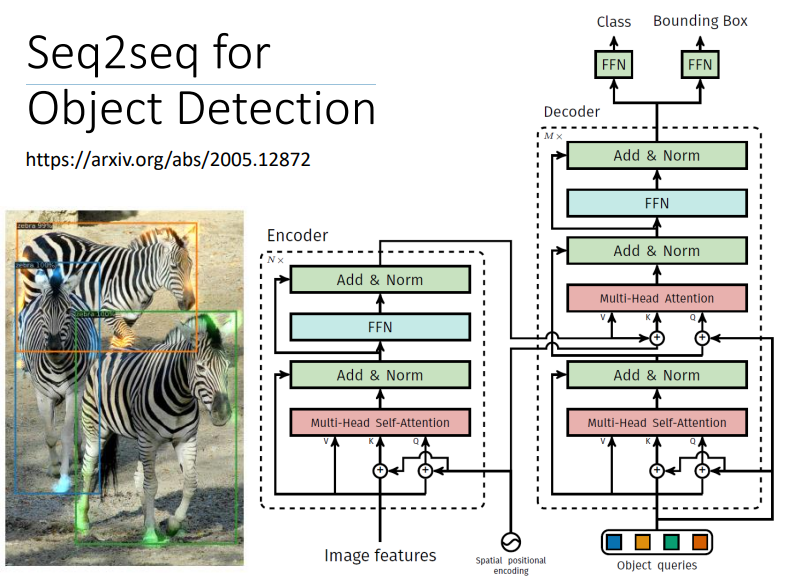
- Seq2seq for Object Detection
Transformer
Encoder-Decoder架构
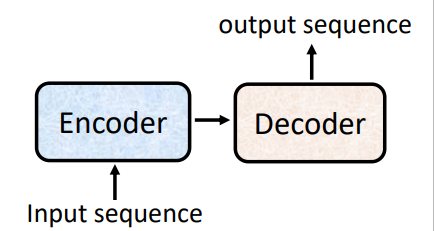
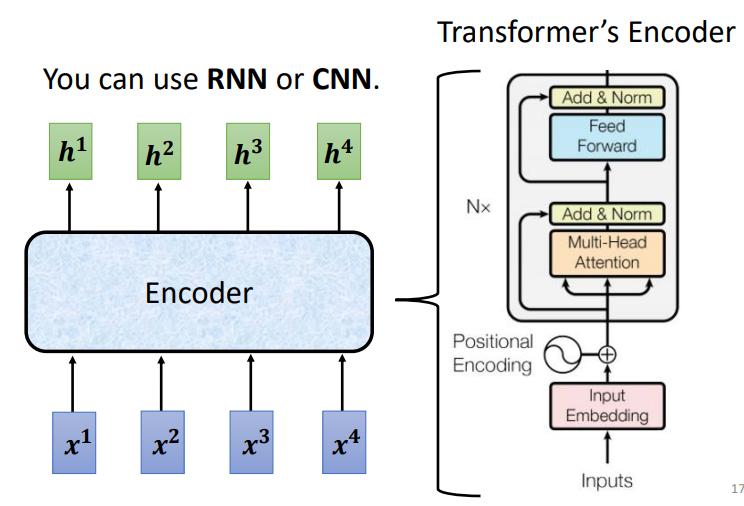
结构
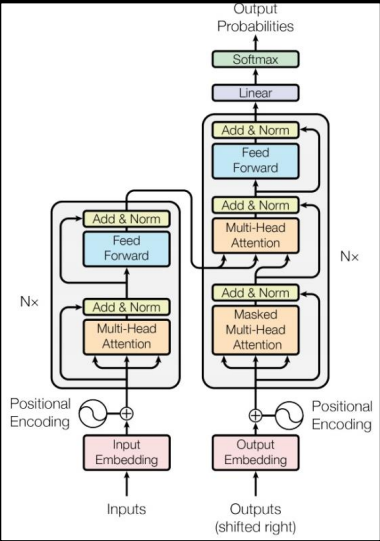
Encoder
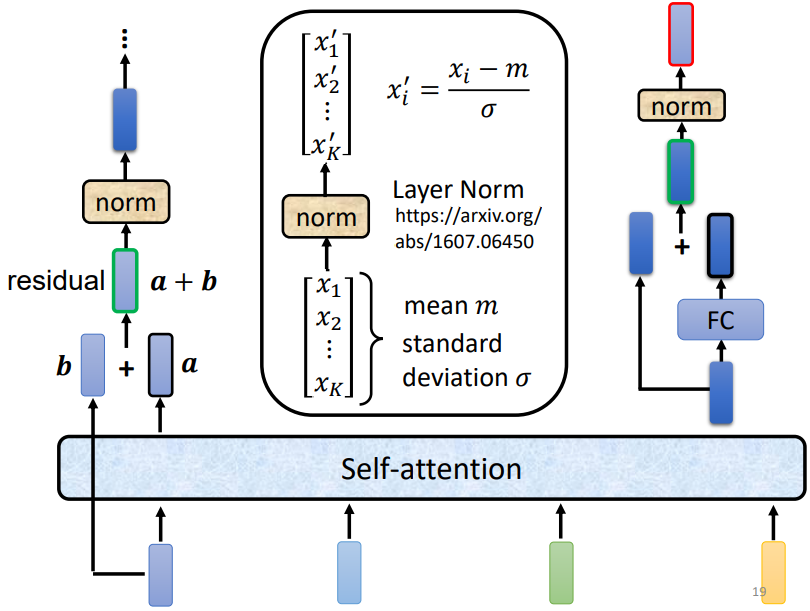
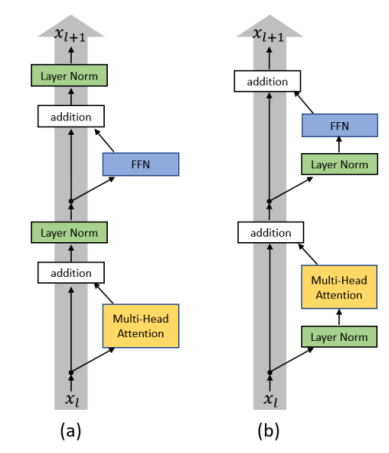
Layer Norm的调整
Decoder
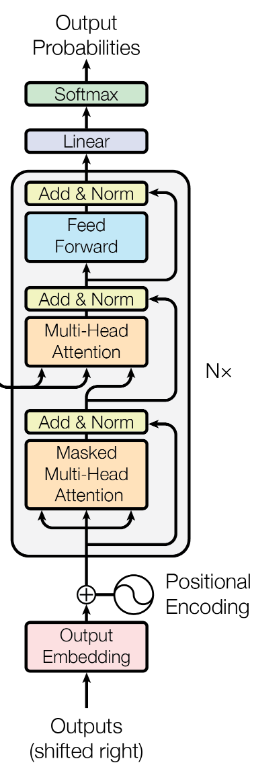
Transformer的Decoder是一个自回归的Decoder(Autoregressive Decoder)
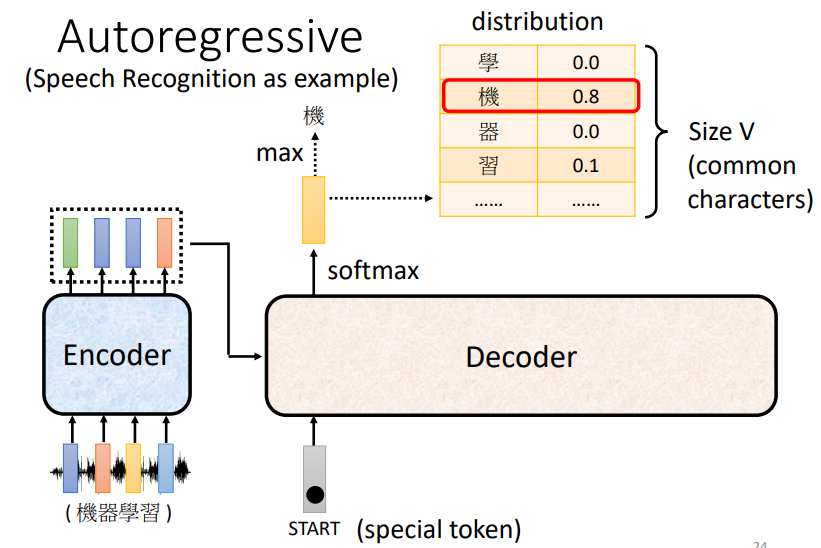
Masked Self-attention
- 在解码器中,第一个注意力机制是一个掩码的自注意力
- 这是因为解码器需要输出一个序列,它需要在不知道后面的信息的情况下,根据前面的信息,来预测当前的输出
- 所以我们在训练时,需要将后面的序列盖住
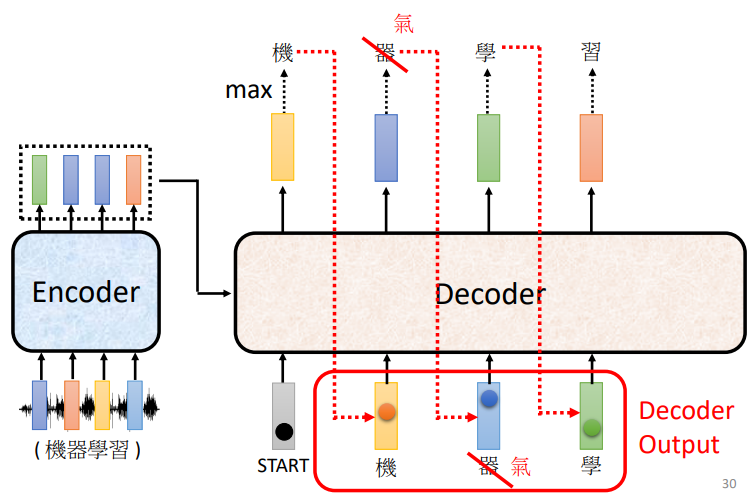
- 在训练时,我们给解码器的输入都是正确答案,帮助其完成训练
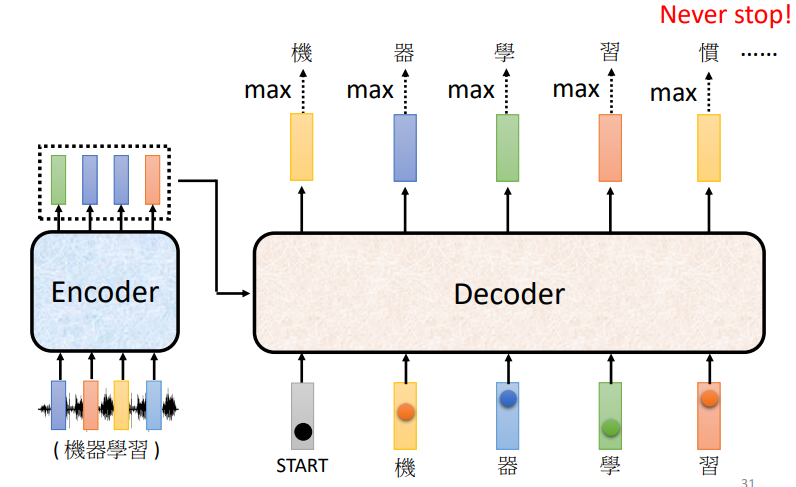
停止符号
为了让输出停止,我们需要定义一个停止符号,提示解码器停止输出
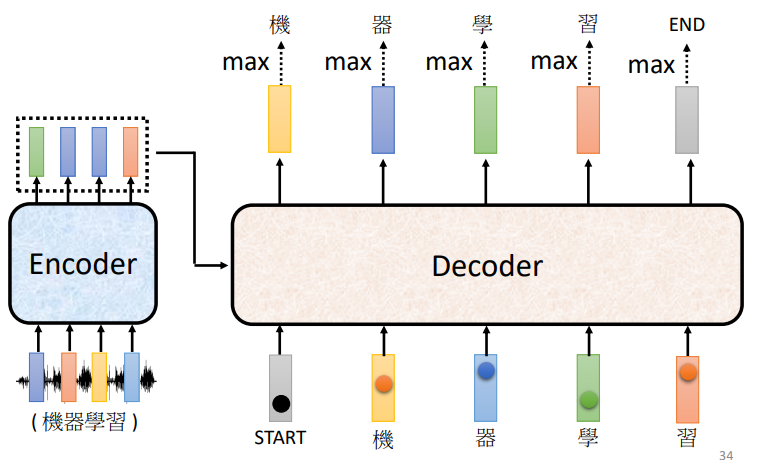
NAT 非自回归
- AT需要前面的输出信息,才能给出当前的输出
- NAT可以并行地给出输出,速度比AT要快,生成更加稳定
NAT解码器如何决定输出的长度
- 预测输出序列的长度(predictor)
- 输出一个固定长度的长序列,忽略终止符END后面的Token
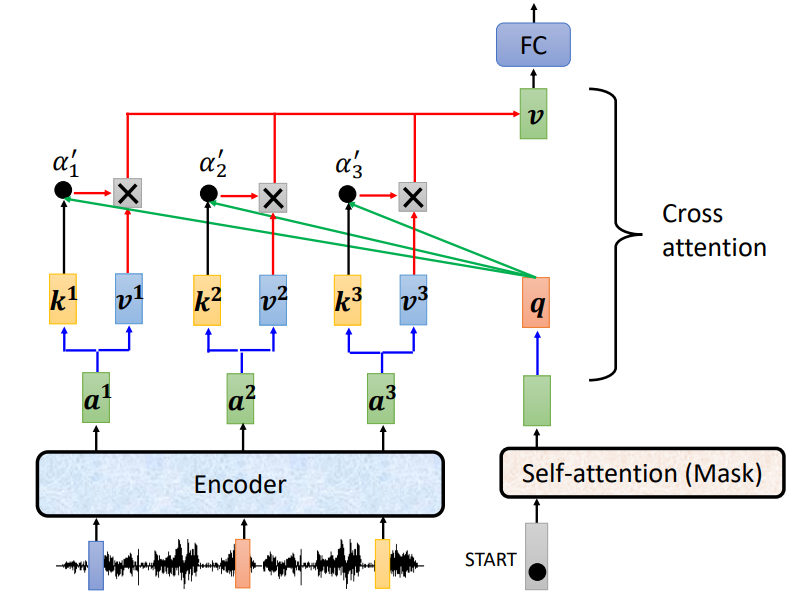
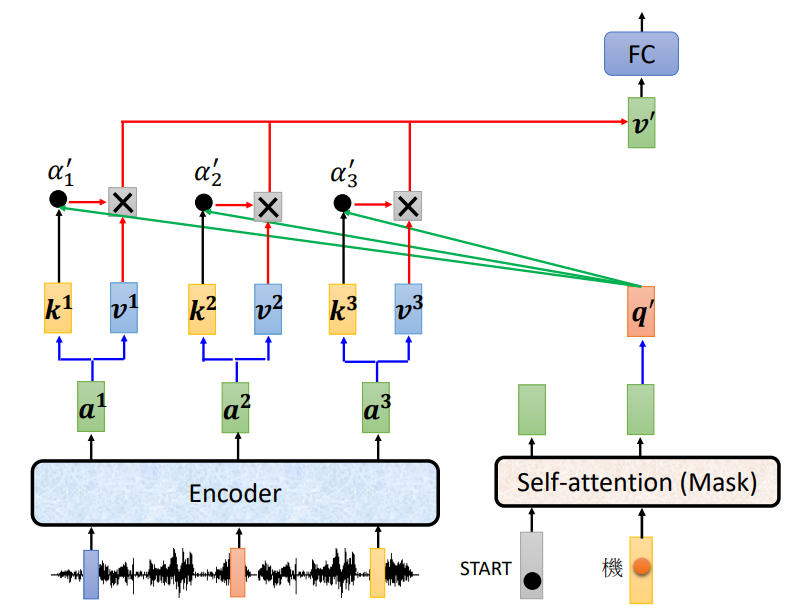
Cross attention
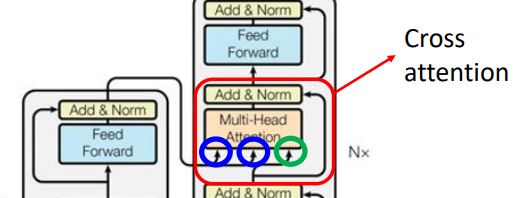
Cross attention部分会将Encoder的最后一个输出转换为Decoder部分的\(k\)和\(v\)矩阵
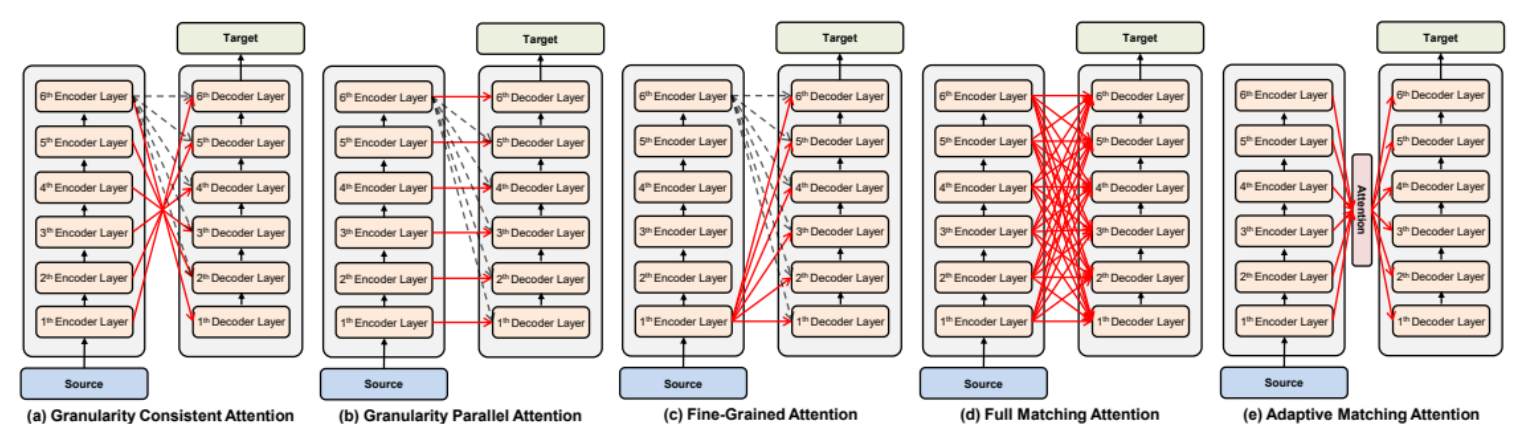
不同的连接方式
训练Transformer
- Encoder和Decoder联合训练
- 使用softmax和cross entropy进行训练
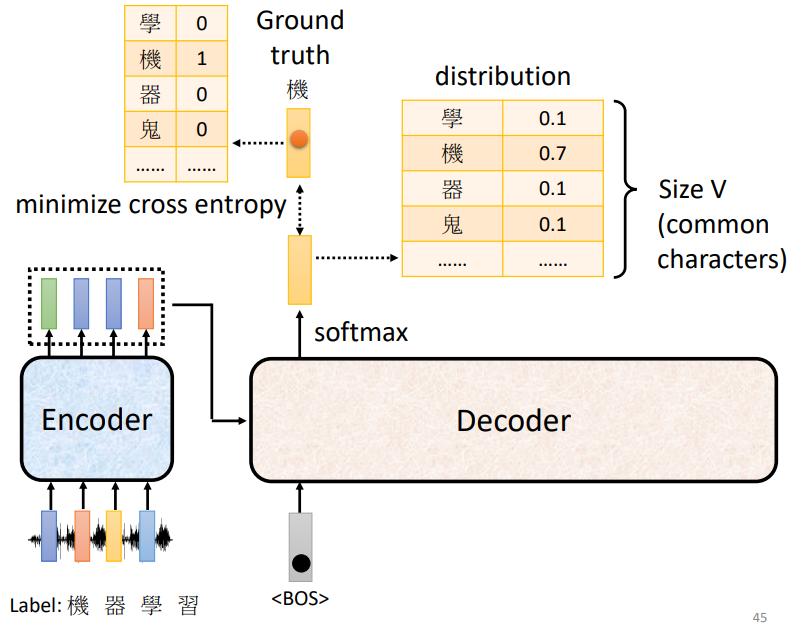
Teacher Forcing模式
将输出数据作为Decoder的输入,使其向正确输出靠近
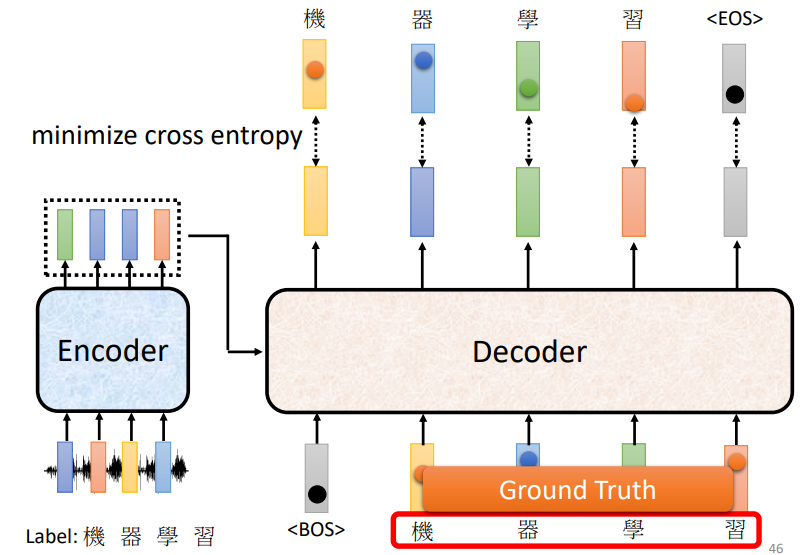
Tips
Copy Machanism 复制机制
将一些不太需要翻译的人名、地名等直接复制

Guided Attention
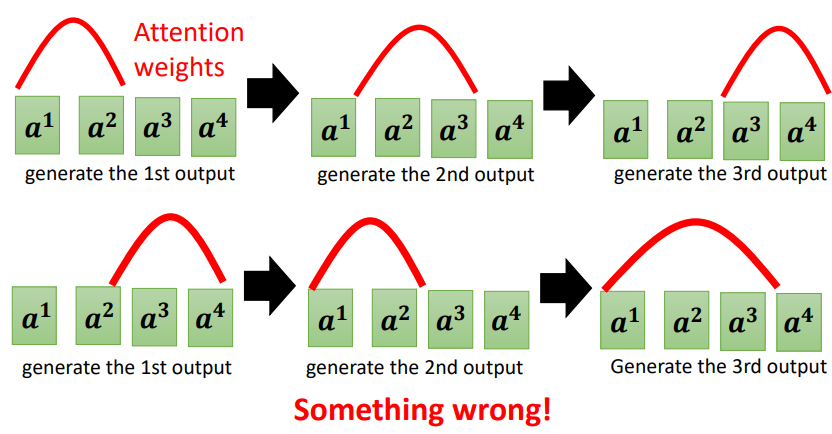
Monotonic Attention
Location-aware attention
在一些任务中,输入和输出是单调排列的,顺序关系不可改变
例如下面的序列中,在输出时,第一个输出中,Attention关注的是后面的序列
Beam Search
- 在Attention Score中,模型会选择当前分数最高的,但是多次选择后,综合起来,不一定是最好的选择
- Beam Search会综合考虑全局的分数,选择最好的结果
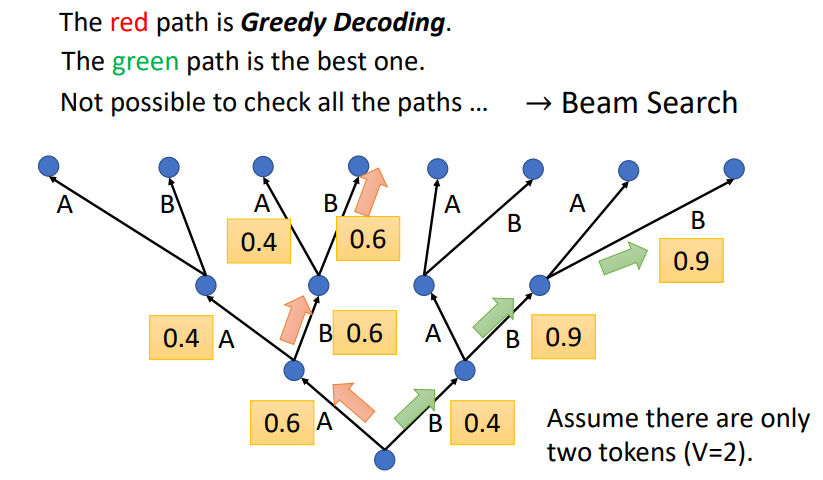
但是最好的选择不一定会产生很好的结果
Sampling

在一些任务中,生成序列时,Decoder需要一些噪声(Randomness),sample是指从某些分布中sample中出来的噪声
Scheduled Sampling
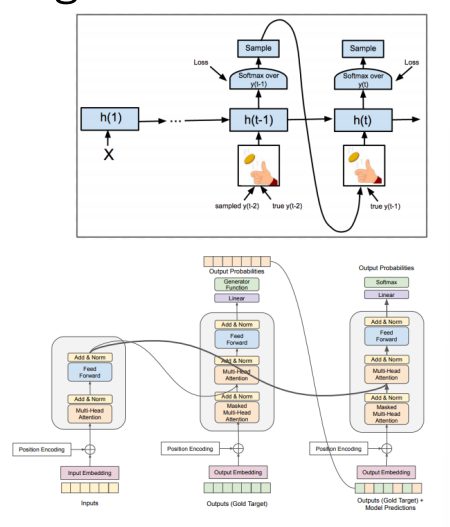
采样由Decoder决定
Optimizing Evaluation Metrics
优化方案的选择
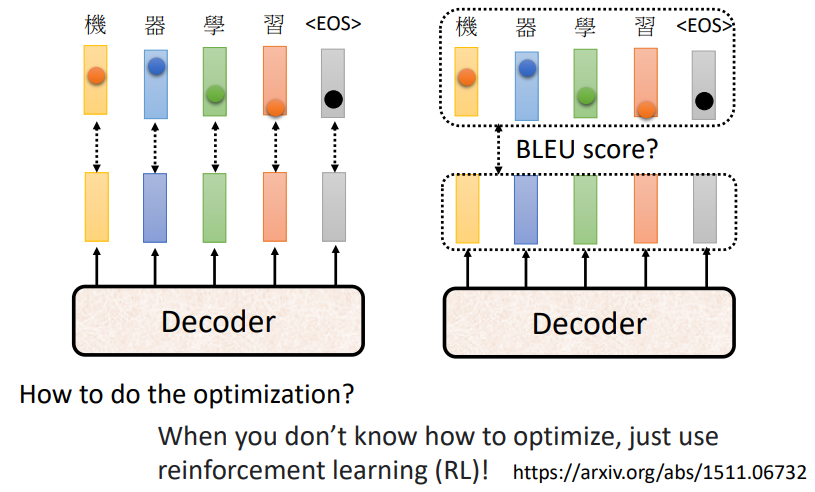
- Cross Entropy
- BLEU score
- Reinforcement learning
各种各样的Attention
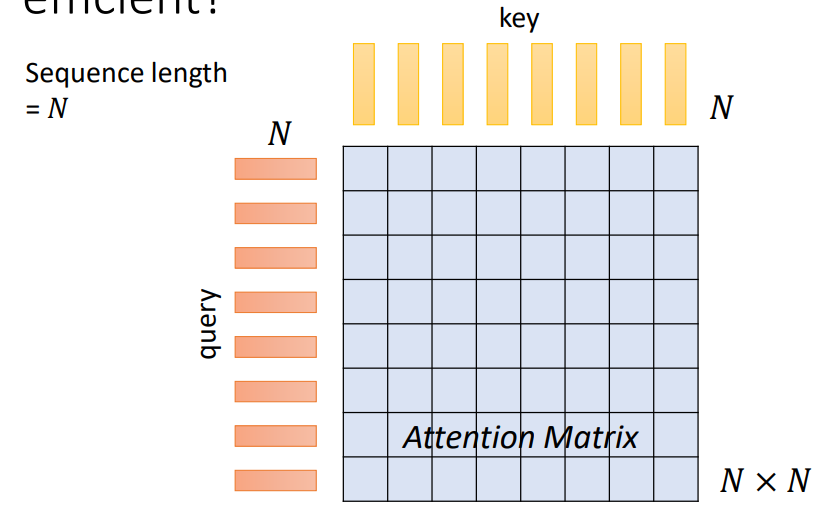
自注意力机制的运作
- 利用Query和Key构造一个Attention Matrix
- 自注意力只是一个大型网络的一个模块
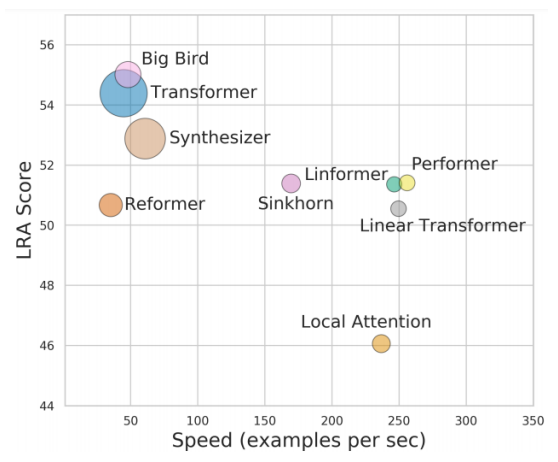
- 当序列的长度N足够大的时候,自注意力在计算占主导
- 通常用于图像处理
人工干预来跳过一些Attention Matrix的计算
Local Attention/Truncated Attention
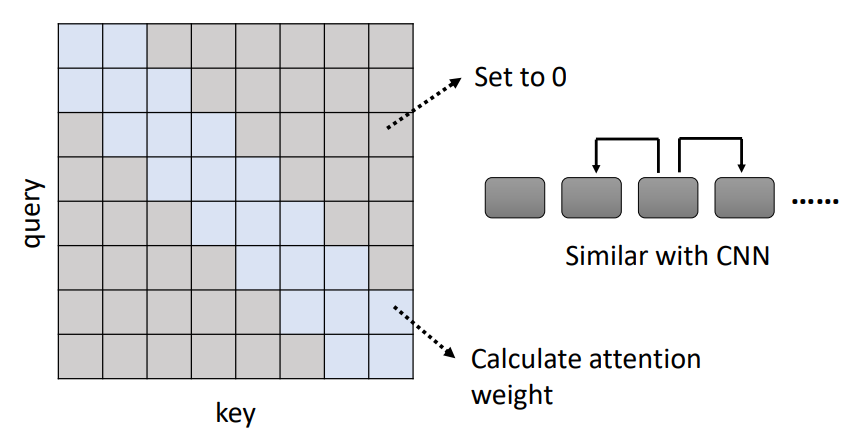
- 只计算标记的部位,其他位置设置为0
- 跟CNN有些相似
Stride Attention
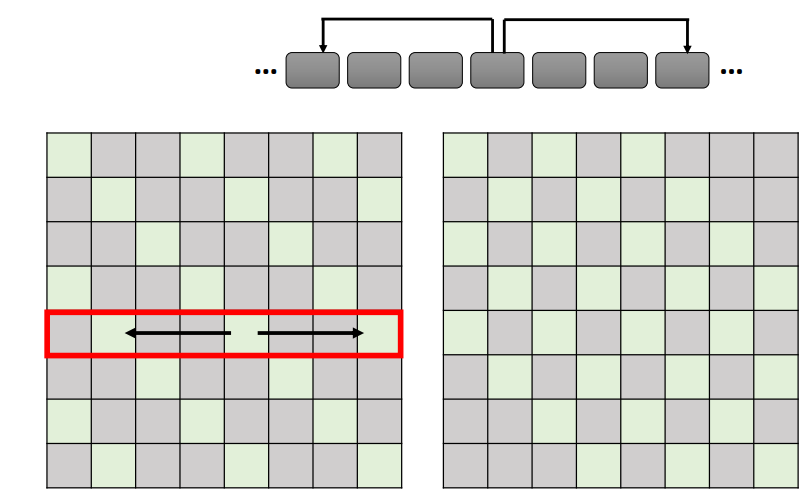
- 选中从自身向左右两边跨越规定的步数的部位,进行计算
Global Attention
- 在原来的序列中添加special token
- 关注(attend)每一个token,可以收集全局信息
- 被每一个token关注(attend),知道全局信息

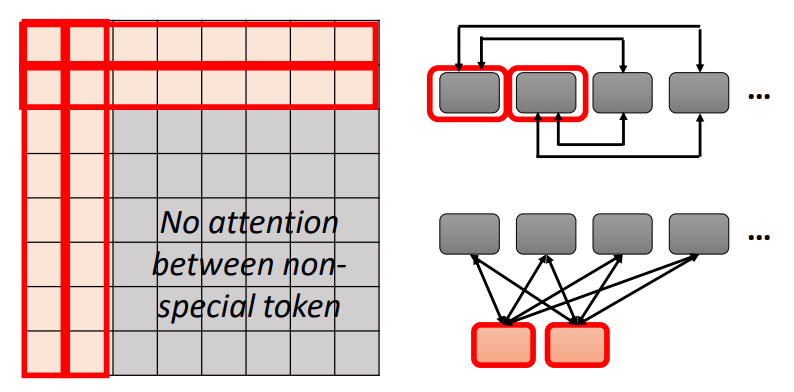
图中前两个是special token
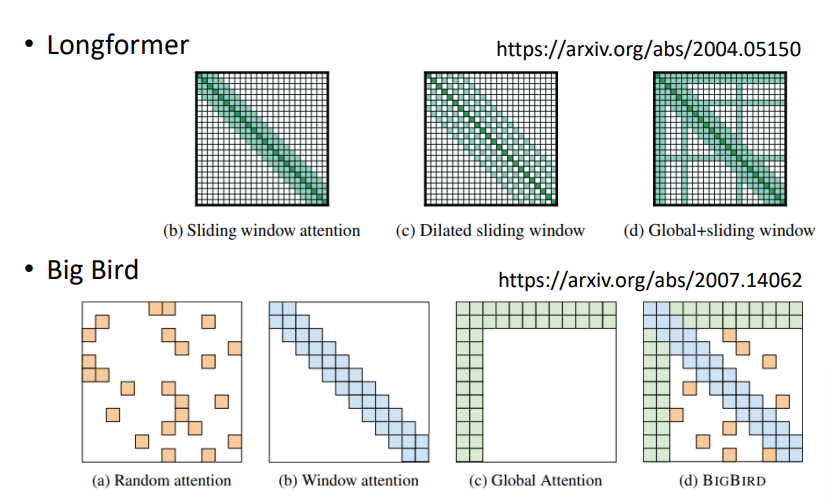
小结
- 可以在一个模型中同时使用不同的Attention
- 不同的head可以使用不同的模式
关注一些Matrix中关键的部分(Critical Parts)
- 小数值直接设置为0
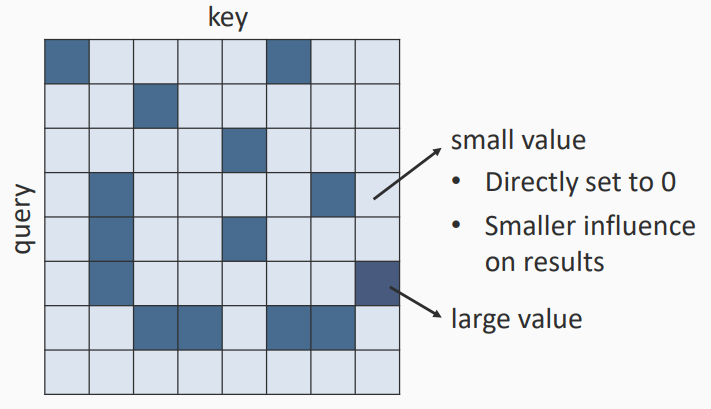
- 如何快速估计注意力权重较小的部分
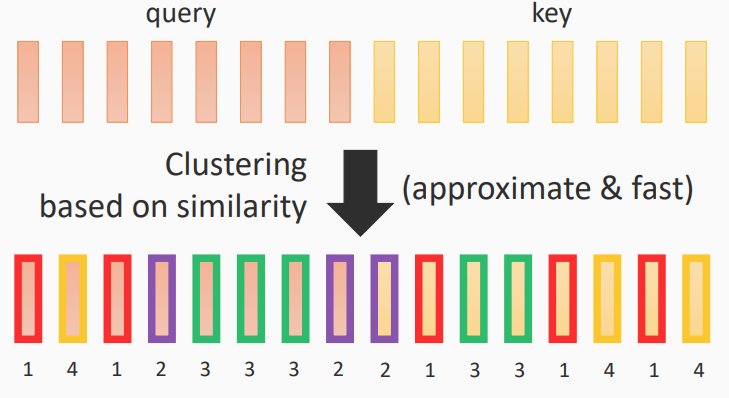
Clustering
- Reformer
- Routing Transformer
步骤1
基于相似度对query和key进行聚类标注
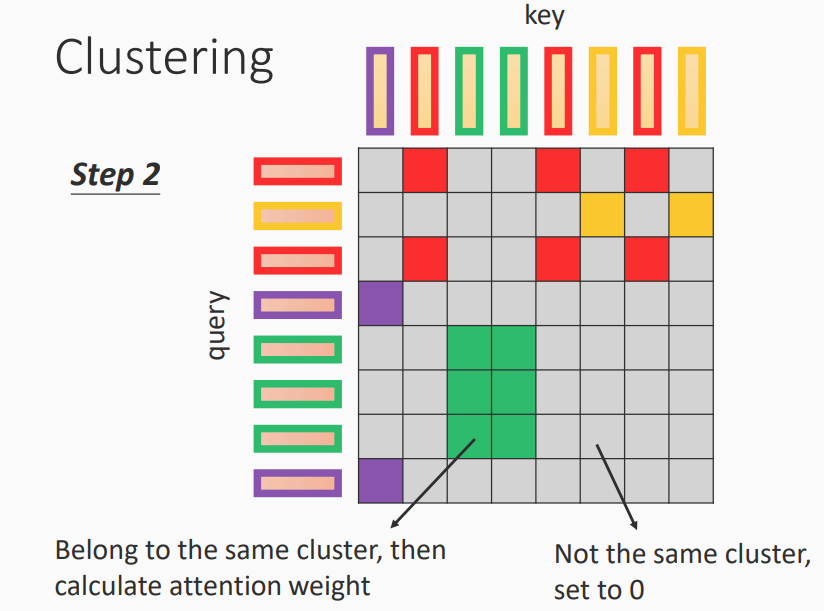
步骤2
- 相同类别的才计算attention weight
- 不同类别的设置为0
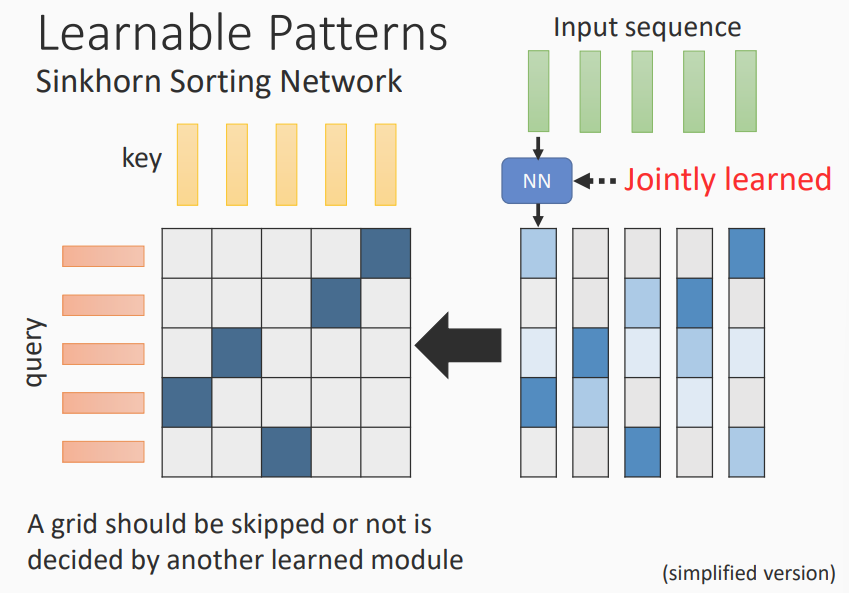
Learnable Patterns
通过学习来获取需要计算的部位
不需要完整的Attention matrix
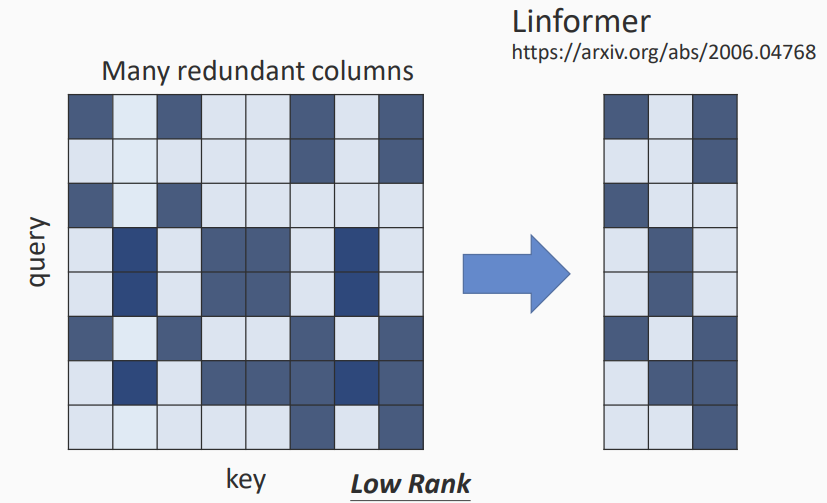
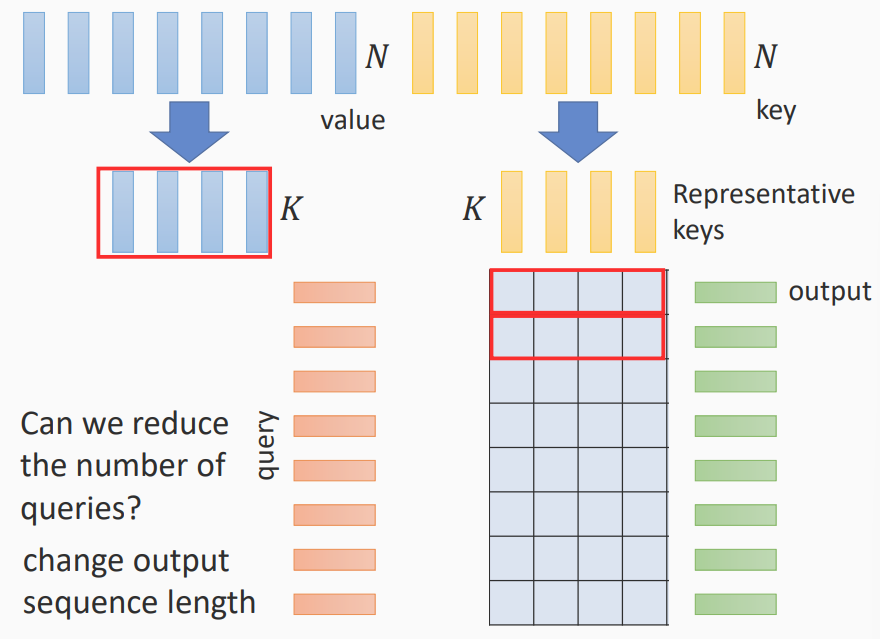
- 可以减少key和value的长度
- query的长度不变,因为输出长度需要不变
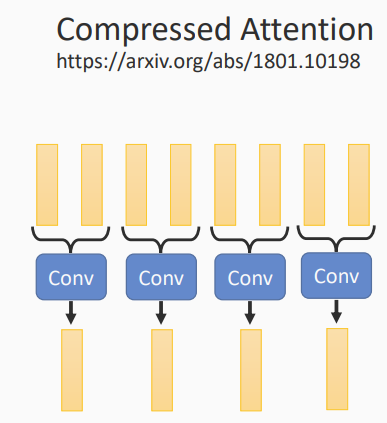
使用卷积
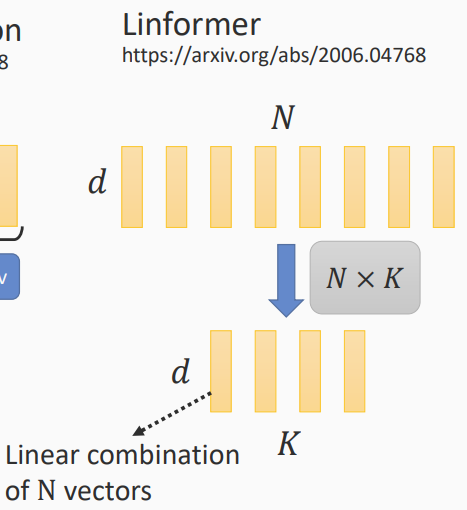
使用参数矩阵相乘
注意力机制计算
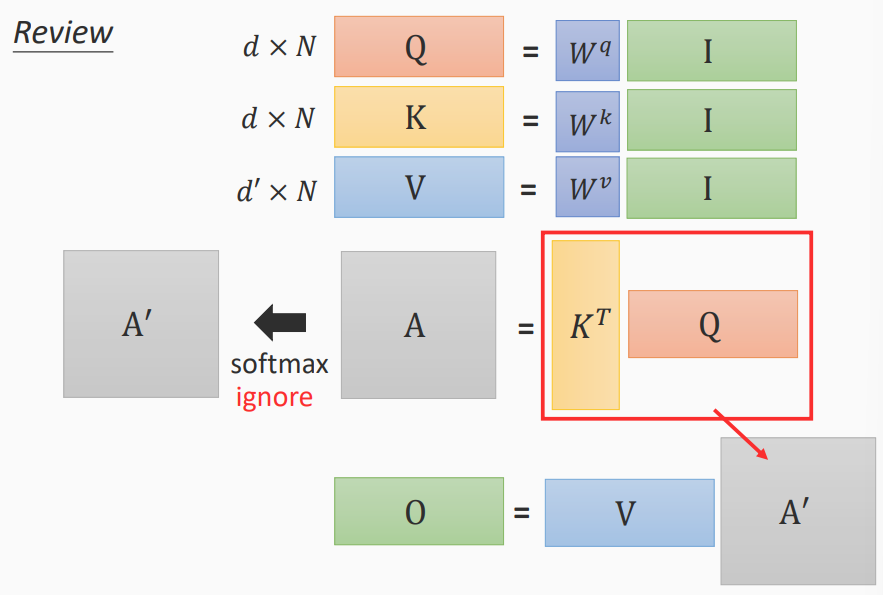
- 利用输入I获取Q、K、V进行运算,得到输出O
- 为加快运算,采用矩阵计算的形式
计算方式的不同
- \(K^TQ\)先计算
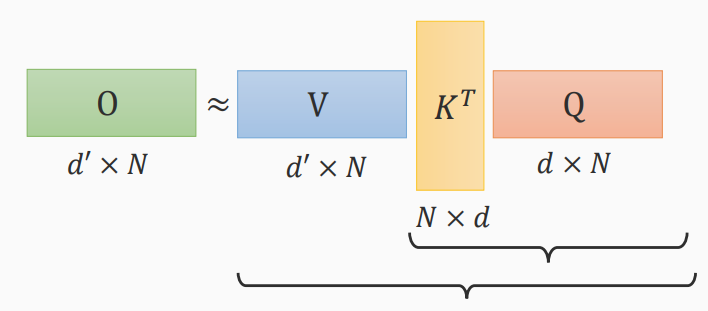
- \(VK^T\)先计算
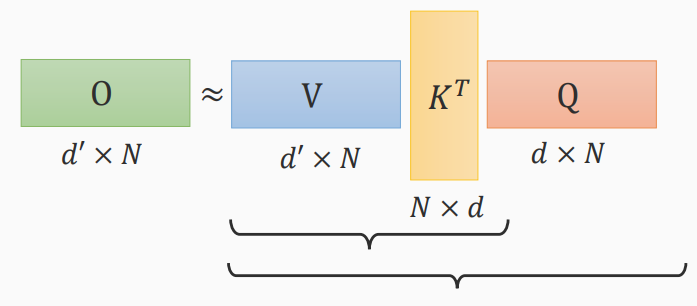
三个矩阵计算顺序不同,进行乘法次数不同,结果相同

而Q、K、V三个矩阵的运算中,
正常进行计算,会进行\((d+d^\prime)N^2\)次乘法运算
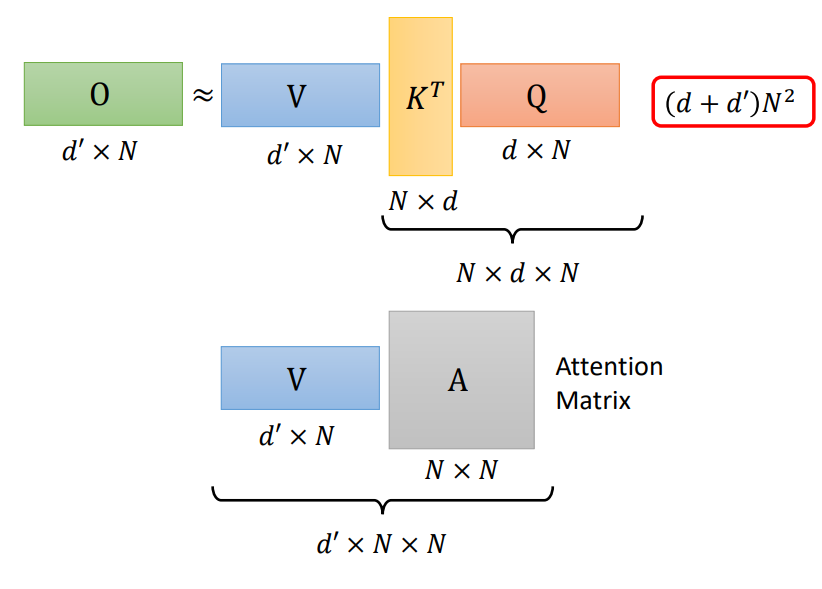
先计算\(V K^T\)的话,会计算\(2d^\prime dN\)次乘法运算,小于正常运算次数,序列长度N是大于维度d的
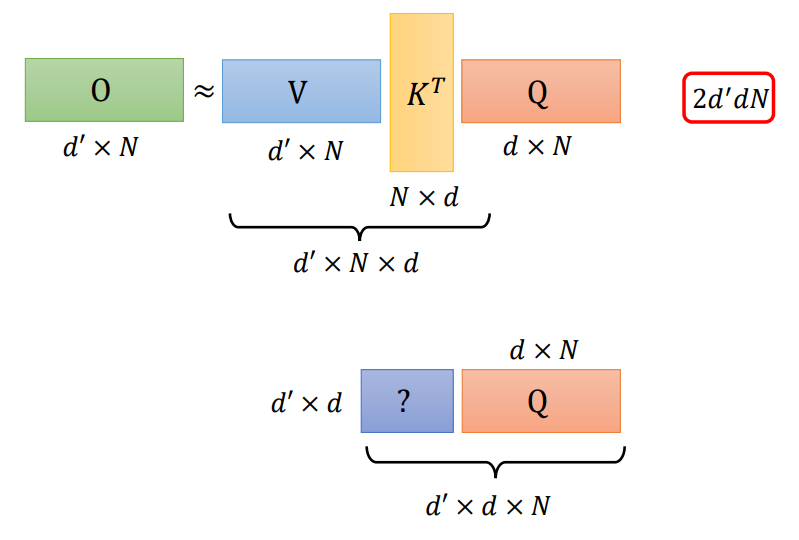
注意力计算的变换
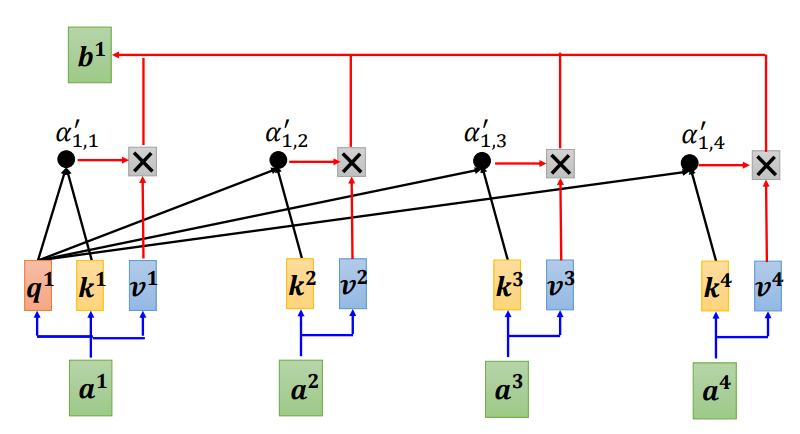
我们利用当前向量的\(q\)矩阵,来与自身和其他向量的\(k\)矩阵进行运算,再经过\(softmax\)运算,得到\(\alpha^{\prime}\),即 \[ \alpha^{\prime}_{1,i} = \sum_{i=1}^{N}\frac{exp(q^1\cdot k^i)}{\sum^N_{j=1}exp(q^1\cdot k^j)} \] 这里以\(a^1\)向量(\(q^1\)矩阵)为当前向量。
再将得到的\(\alpha^{\prime}\)与对应的\(v\)矩阵进行运算,合成起来得到\(b^1\),即 \[
b^1 = \sum_{i=1}^{N}\alpha^{\prime}_{1,i}v^i =
\sum_{i=1}^{N}\frac{exp(q^1\cdot k^i)}{\sum^N_{j=1}exp(q^1\cdot k^j)}v^i
\]
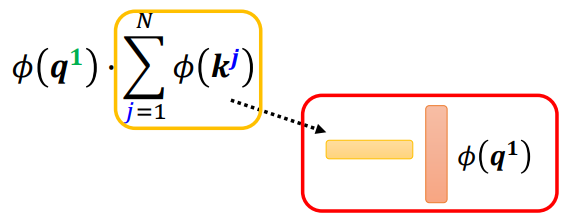
在这里,我们可以对\(softmax\)的计算进行改变 \[
exp(q\cdot k) \approx \phi(q) \cdot \phi(k)
\] 这里的\(\phi\)是一个变换,那么\(b\)的计算可以变换为 \[
\begin{equation}
\begin{aligned}
b^1 = \sum_{i=1}^{N}\alpha^{\prime}_{1,i}v^i
&=\sum_{i=1}^{N}\frac{exp(q^1\cdot k^i)}{\sum^N_{j=1}exp(q^1\cdot
k^j)}v^i \\ \\
&=
\sum^N_{i=1}\frac{\phi(q^1)\cdot\phi(k^i)}{\sum^N_{j=1}\phi(q^1)\cdot\phi(k^j)}v^i
\\ \\
&=
\frac{\sum^N_{i=1}\phi(q^1)\cdot\phi(k^i)v^i}{\sum^N_{j=1}\phi(q^1)\cdot\phi(k^j)}
\end{aligned}
\end{equation}
\] 而分母项可以进一步进行调整 \[
\begin{equation}
\sum^N_{j=1}\phi(q^1)\cdot\phi(k^j) = \phi(q^1)
\cdot\sum^{N}_{j=1}\phi(k^j)
\end{equation}
\]
那么\(b^1\)的计算进一步调整
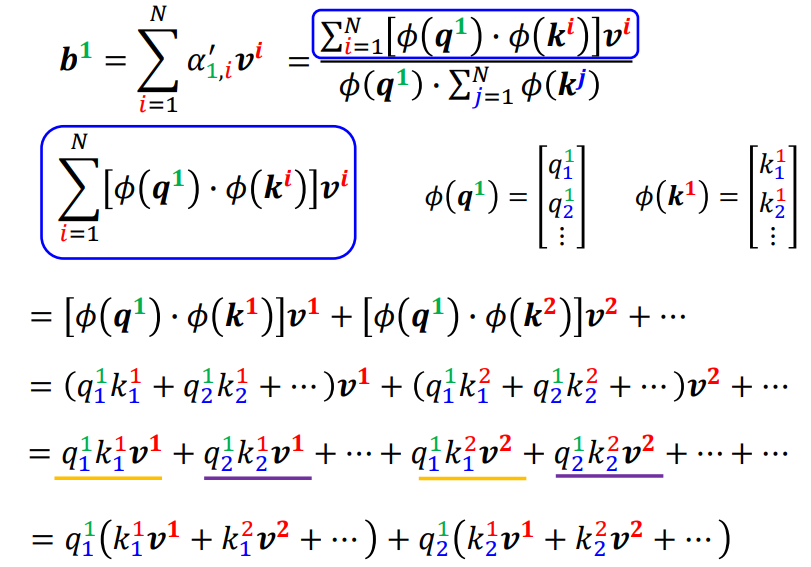
我们可以利用\(k\)和\(v\)提前计算好部分值,需要时直接调用即可
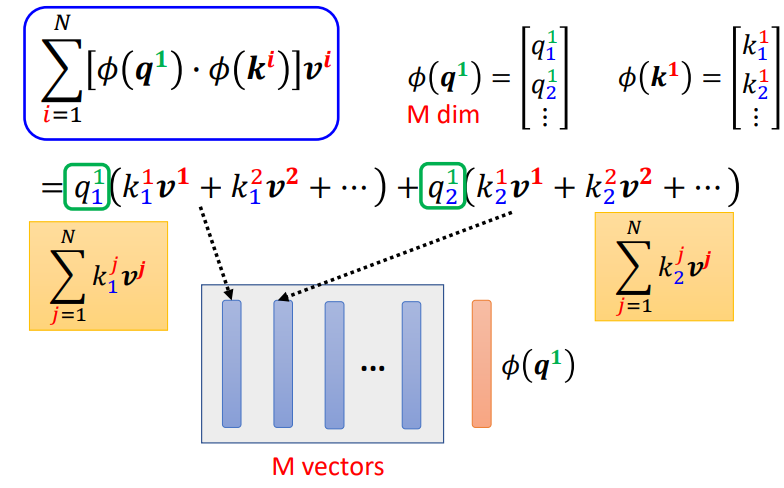
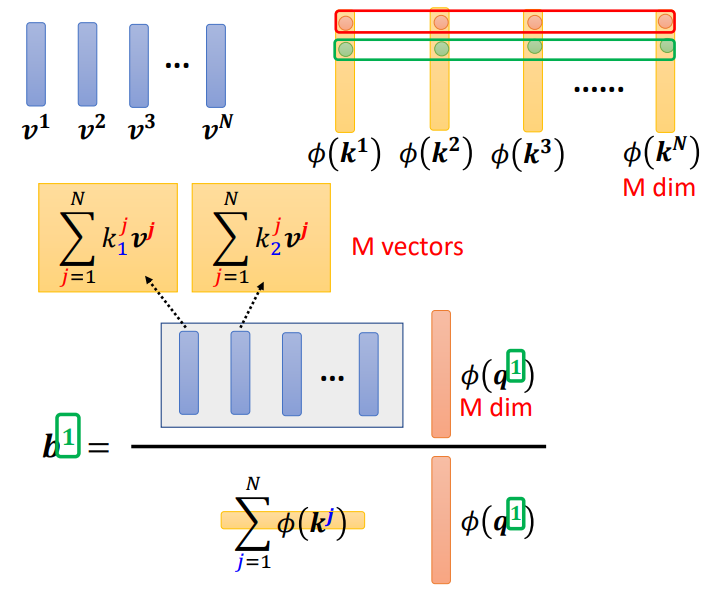
这样子,有一部分不用重复进行计算
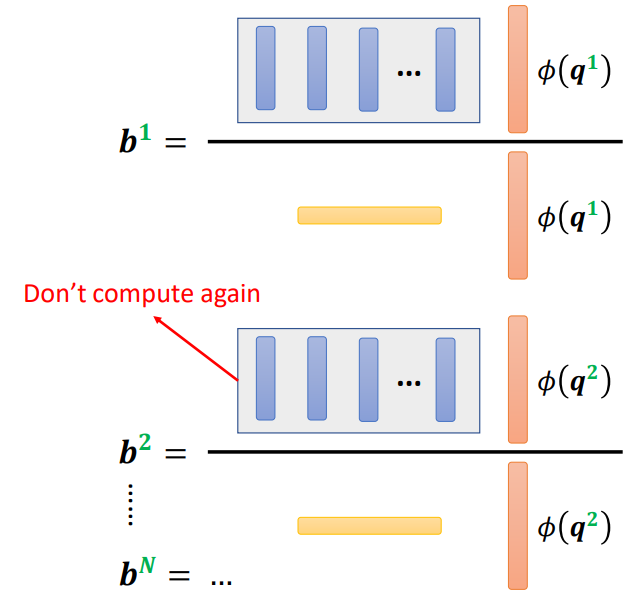
这样利用\(\phi(k)\)和\(v\)计算出来的M组向量相当于有M组模板,\(\phi(q)\)与之相乘是在进行选择。
通过学习来构造Attention Matrix
注意力机制通过\(q\)和\(k\)来计算Attention Matrix,但是我们可以将整个矩阵是为网络的参数

小结
